C-Element
Finally, after introducing the basics of concepts, we can now apply this to the design of logic gates. In this post, we will produce a very standard gate, a C-Element.
A C-Element’s basic operation is that, when all the inputs to the gate are high, or 1, then the output will be set high. This output will remain high until all of the inputs are low, or 0, at which point the output will be set low.
So let’s describe this using concepts!
Concepts
For this example, the C-Element we describe will be a 2 input gate. These will be a and b. The single output will be c.
So let’s start with describing what causes the output to go high:
outputRise = a+ ⇝ c+ ⋄ b+ ⇝ c+
This concept will cause the output, c, to go high when both the inputs, a and b, are high.
Next, let’s describe what causes the output to go low:
outputFall = a- ⇝ c- ⋄ b- ⇝ c-
Similar to the previous concept, outputFall will cause c to go low only when both a and b are low.
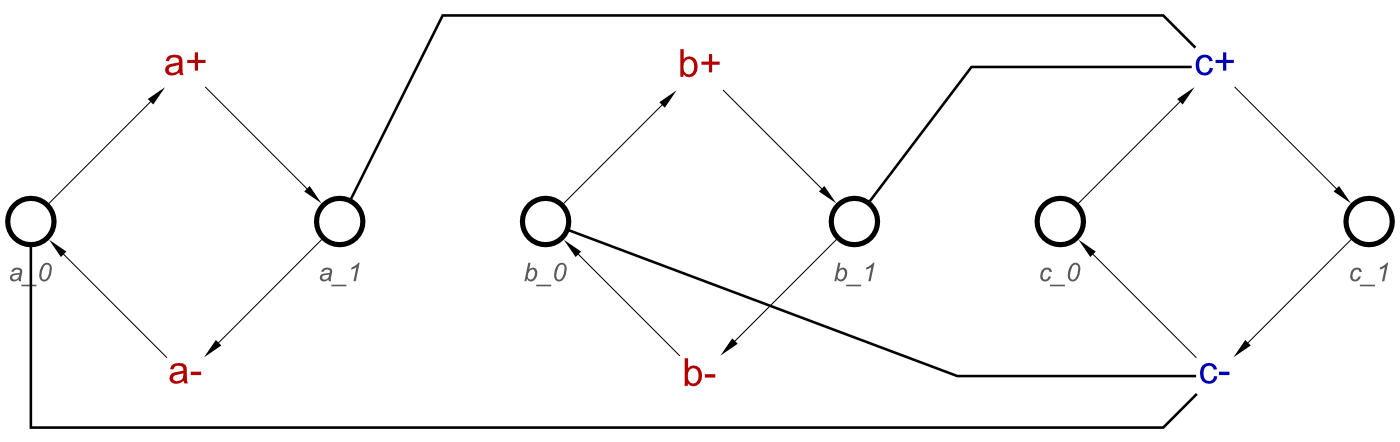
And these two concepts describe the operation of a C-element. Let’s combine them, and then we can Convert them to an STG, giving us the following:
C-Element = outputRise ⋄ outputFall
In this state however, this STG is not particularly useful, as there are no initial states, and therefore it cannot be simulated or synthesized. Thus, let’s add an initial state concept:
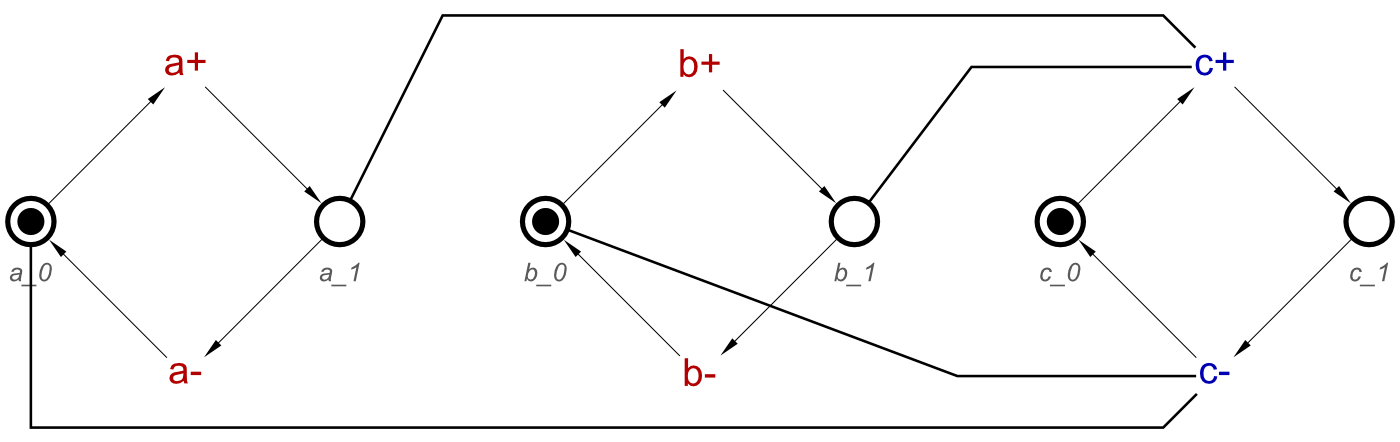
initialState = initialise(a, 0) ⋄ initialise(b, 0) ⋄ initialise(c, 0)
CElement = outputRise ⋄ outputFall ⋄ initialState
By setting all the initial states to 0, we can then test this STG using Workcraft, and see that the STG (shown below) operates as a C-element.
This STG could also be tested by setting the initial states to any combination. The C-Element would still act as expected.
Some reuse
It is possible to describe a C-Element using predefined gates. If we break down some of the concepts used above we find some interesting points.
If we take the interactions of just one input signal and the output signal from the above concepts we get the following:
input1 = a+ ⇝ c+ ⋄ a- ⇝ c-
This concept is actually exactly the same as a gate we have previously defined: a buffer. Thus, a C-Element can actually be described using these:
CElement = buffer(a, b) ⋄ buffer(b, c) ⋄ initialState
The initial state must be included in order for the resulting STG to be usable in further operations.
Finally
This blog post has finally explained how concepts can be used to design a logic gate, albeit a simple one. This includes describing it’s operations in terms of the interactions of the input and output signals, or using predefined concepts, particularly a buffer.
The next post will continue in the effort to define logic gates using behavioural concepts, the next being an Set-Reset Latch.