OR-causality is an interesting part of specification of circuits, specifically when using Signal Transition Graphs (STGs). We have recently released a translation tool for Concepts (available from https://github.com/tuura/concepts), which will take a set of concepts, and produce an STG specification for this. This includes both standard AND-causality, and OR-causality. OR-causality poses a challenge, as with STGs, and in this post we aim to discuss this.

This will be a 2 part series, with several examples to help explain OR-causality in this post, part 1, and an algorithm in part 2 to translate OR-causality concepts to STGs.

OR-causality, an introduction

For this, let’s use four simple examples. Here, we will assume initial states for all signals as 0.

1. OR-Gate

A standard gate used in many applications, an OR-gate, and the associated causality,  is important and a good example to use to display OR-causality.

In concepts, an OR-gate is defined as follows:

orGate a b c = [a+, b+] ~|~> c+ ⋄ a- ⇝ c- ⋄ b- ⇝ c-

There are some operators to discuss here:

[a+ , b+] – This is how signal transitions are listed.
~|~> – This shows an OR-Causalilty relationship

In words, this is a composition of three concepts. First, either a+ or b+ cause c+. Then, a- causes c-, and b- causes c-.

This will mean that, when a+,  b+ or both of these occur, c+ can occur. But, for c- to occur, a- and b- must have occurred.

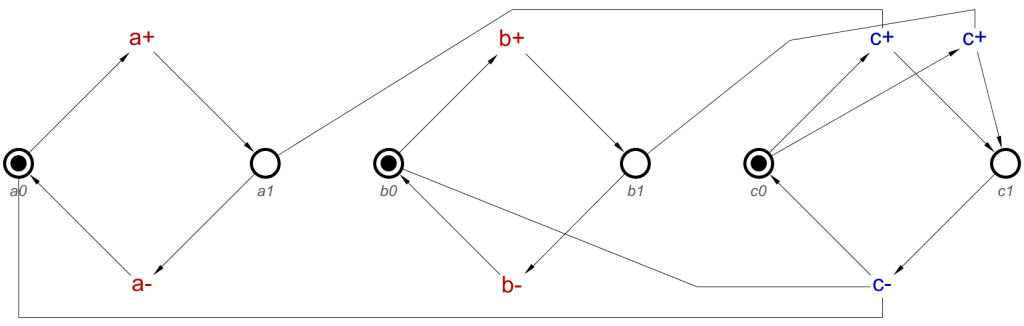
This is the STG produced from translating the OR-gate concept. This looks like any other STG we have shown on this blog, however notice that there are two c+ transitions. This is how OR-causality is displayed in STGs. When a+ occurs, one of the c+ transitions can occur. When b+ occurs, the other c+ transition can occur. If both a+ and b+ have occurred, then either of the c+ transitions can occur. However, both a- and b- can occur, then and only then can c- occur.

Notice, that for the c+ transition, there is OR-causality with a+ or b+, but for the c- transition, there is AND-causality with a- and b-.

2. OR-Gate with a single AND-causality

This is an OR-gate with inputs a and b, and output c, with another input signal d. d will form a buffer with c, including some AND-causality as well. This way we can show how AND- and OR-Causality interact. In concepts this is:

circuit  = orGate a b c ⋄ buffer d c

And, expanded into signal-level concepts, this is:

circuit = [a+, b+] ~|~> c+ ⋄ a- ⇝ c- ⋄ b- ⇝ c- ⋄ d+ ⇝ c+ ⋄ d- ⇝ c-

In words, for c+ to occur, d+ must occur, and either b+ or c+. For c- to occur, all of a-, b- and d- must occur.

So, as a thought experiment, if a+ and b+ have occurred, no c+ transition can occur without d+ having occurred.

The STG after translating the above concept is: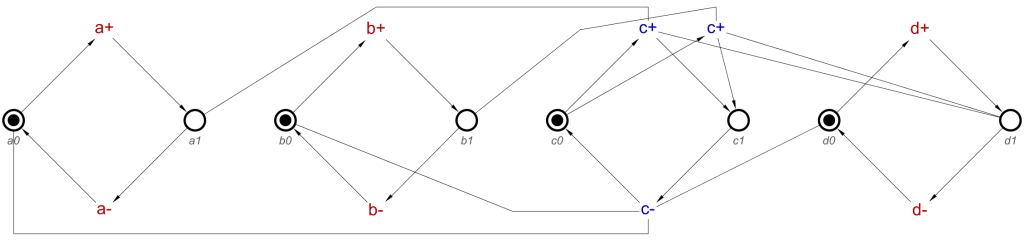

Notice that this looks similar to the previous image, but with an extra consistency loop for the signal d. However, notice that d1, the place showing when d+ has occured, is connected to both c+ transitions. And d0 is connected to c-. This will therefore mean that, regardless of which of a+ or b+ have occured, c+ cannot occur without d+ occuring.

3. AND-Gate

Another standard gate. In this case, when thinking of it in terms of causality, it is the opposite of the OR-gate. i.e. For the c+ transition, there is AND-causality with both the a+ and b+ transition. Yet, with the c- transition, there is OR-causality between the a- and b- transitions.

The concepts for this is:

andGate a b c  = a+ ⇝ c+ ⋄ b+ ⇝ c+ ⋄ [a-, b-] ~|~> c-

This can be described in words as in the previous paragraph.

Let’s translate this to an STG.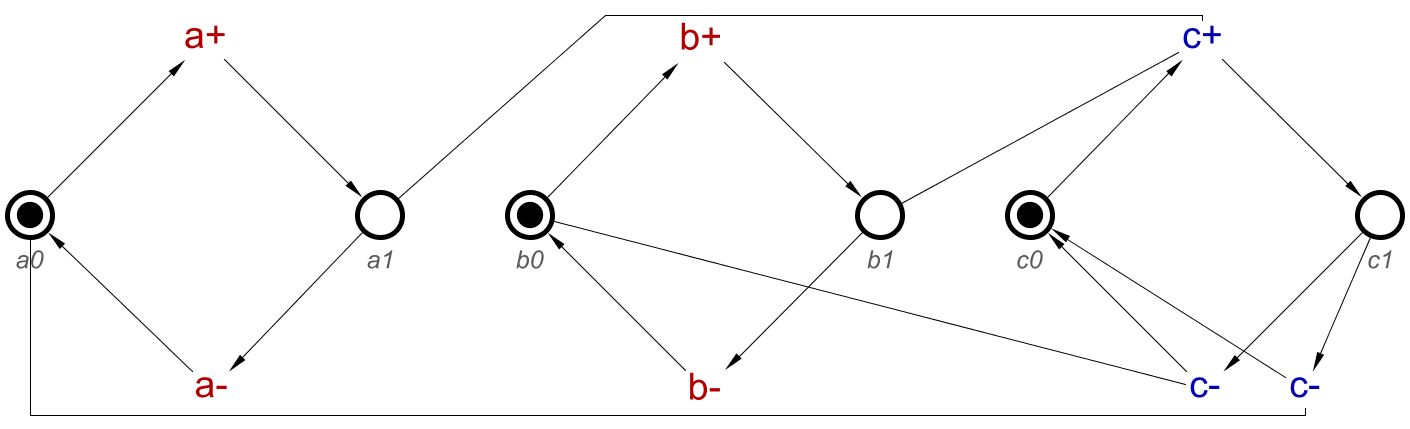

Notice that this time, there are two c- transitions, as this transition is the OR-causality in an AND-gate. Notice the similarities between this and the OR-gate STG, just a sort-of mirror image.

4. AND-Gate and OR-Gate

For this, signals a and b are the inputs to an OR-gate, and signals d and e are the inputs to an AND-gate. The outputs for both of these gates are c. Synthesizing this would not simply produce an AND and OR gate, but for this example, it shows how the AND and OR causality can interact in and interesting way.

This in concepts is:

circuit = orGate a b c <> andGate d e c

If we expand this:

circut = [a+, b+] ~|~> c+ ⋄ a- ⇝ c- ⋄ b- ⇝ c- ⋄
                  d+ ⇝ c+ ⋄ e+ ⇝ c+ ⋄ [d-, e-] ⇝ c-

In words, this means that for c+ to occur, either a+ or b+, and both d+ and c+ must have occured. For c- to occur, both a- and b-, and either d- or e- must have occured.

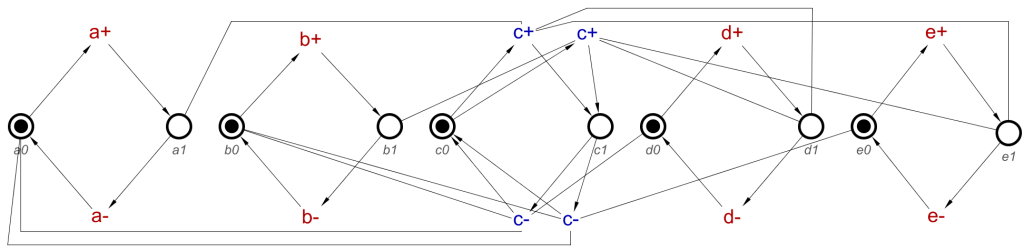
This is slightly more confusing than the previous examples, and the resulting STG produced by translating this concept is interesting:

It does look a little confusing, but notice there are two of both c+ and c- transitions. Their interactions with the other signals determine which of these are able to transition. Testing this would prove that the concept description above works.

Finally

There is little reuse here. The concepts above feature some reuse of previously discussed concepts, but due to the inclusion of OR-causality, we cannot use any previously included gate- or protocol-concept as they do not feature any OR-causality.

So in this post, we have discussed OR-causality, and some uses of it. Specifically, I have aimed to show how it works on it’s own, and in conjunction with AND-causality.

Part 2 of this post will include an algorithm, as we have previously discussed how concepts are translated to STGs, but this algorithm will explain how OR-causality is translated, as this is quite specific.