Category Archives: Inverter

Asynchronous, Buffer, Concepts, Inverter, Latch, Logic Gate, Uncategorised

Concepts V: Set-Reset Latch

Leave a comment

Set-Reset Latch

After learning how a C-element can be produce with concepts, we can introduce other gates. In this case another fairly standard gate, a latch.

The operation of a latch is to hold a given value. There are several different types of latch, but in this case we will talk about a Set-Reset latch (SR Latch). This latch has two inputs, one will set the latch when high, causing its one output to be high. The second input will reset the latch when it is high, causing its output to be low.

So lets see how we can specify this using concepts.

Concepts

For this, let’s start off by referring to the two inputs as a and b. The output is c.

So, first of all, lets think about how we can set the latch:

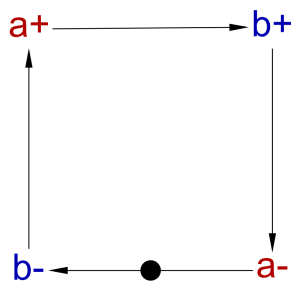
set = a+ ⇝ c+ ⋄ a- ⇝ c-

And it’s that simple. Simply put, when one of the outputs, a in this case, goes high, we want the output, c, to go high.

So we have described the interaction for set using one of the inputs and the output, now lets describe the reset action:

reset = b+ ⇝ c- ⋄ b- ⇝ c+

This will cause the output to go low when the second input, b, goes high.

These two concepts describe the operation of a SR-latch. But we still need to think about how the SR-latch will act initially, such as when it first receives power.

Unless specifically required, we should assume that the output of the latch should be low at startup. Because of this, we don’t want it to be set initially by a being high, so we can set this to 0 initially also.

However, with the second input, b, setting this high at this point would ensure that the output will reset to 0 at start up, but if the initial state of c is already set to low initially, we shouldn’t need to set b to high, so we will set the initial state of this to low too.

The initial state concept will be as follows:

initialState = initialise(a, 0) ⋄ initialise(b, 0) ⋄ initialise(c, 0)

Now let’s create the scenario concept for the SR-Latch:

SRLatch = set ⋄ reset ⋄ initialState

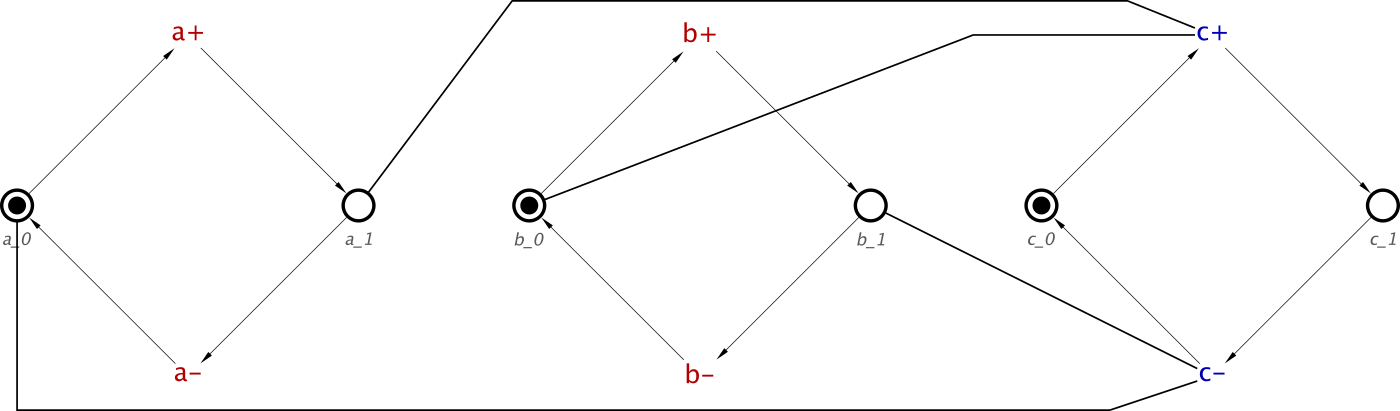
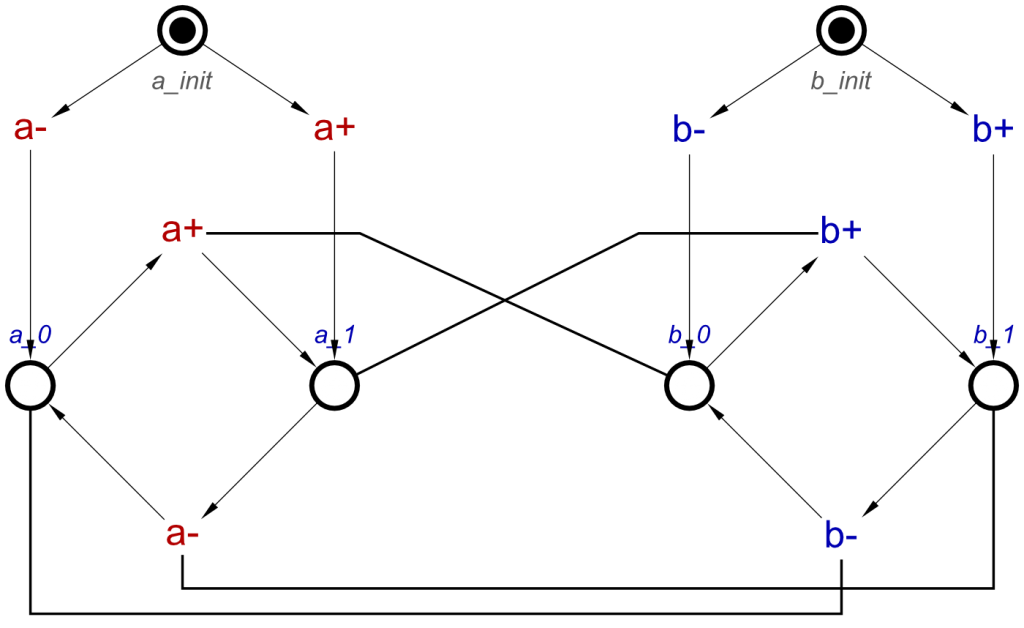
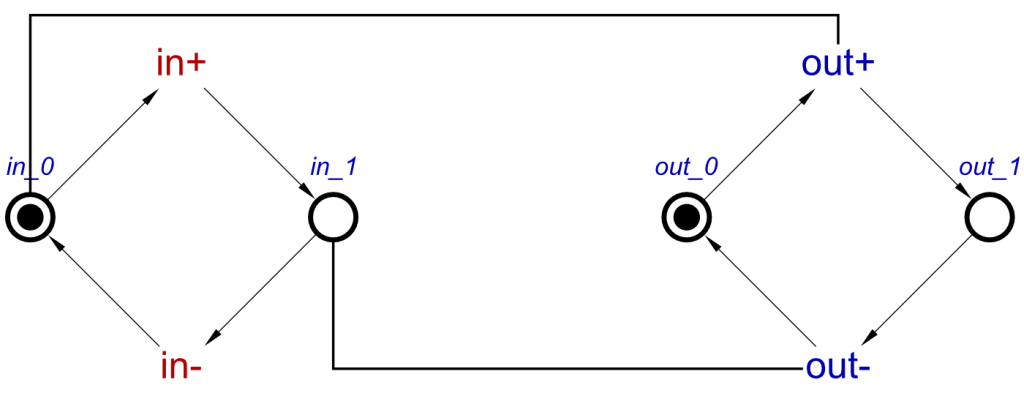
And this can be converted to a Signal Transition Graph, so this specification can be verified, simulated, tested and then synthesised. The STG for a SRLatch will be as follows:

STG_SR_Latch

This is a fairly simple STG, but simulation would prove that setting a high will allow c to transition high. Once it has transitioned high, it cannot transition low until b has been set high.

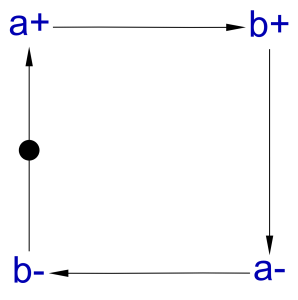
For some simpler understanding of how this latch works, we can change some of the signal names. In this case, we will change a to s, which stands for set. b will be set to r, which stands for reset. Finally, we can call c, q. q is a standard output symbol for latches.

This will change the concepts to the following:

set = s+ ⇝ q+ ⋄ s- ⇝ q-
reset = r+ ⇝ q- ⋄ r- ⇝ q+
initialState = initialise(s, 0) ⋄ initialise(r, 0) ⋄ initialise(q, 0)
SRLatch = set ⋄ reset ⋄ initialState

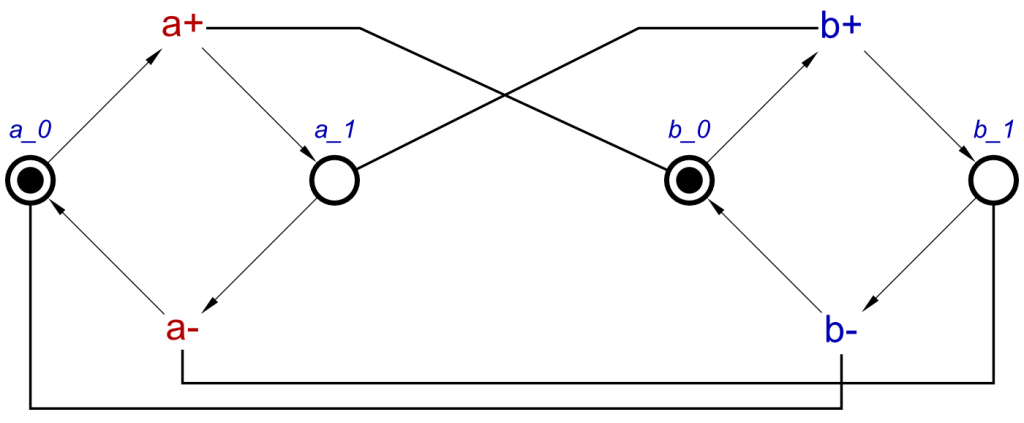
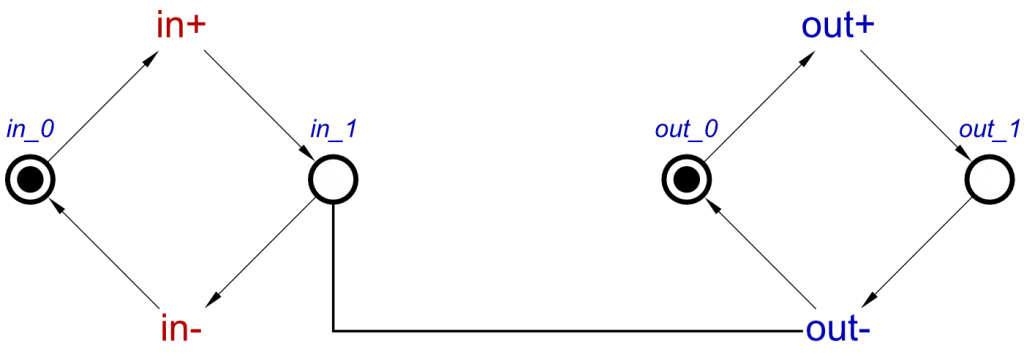
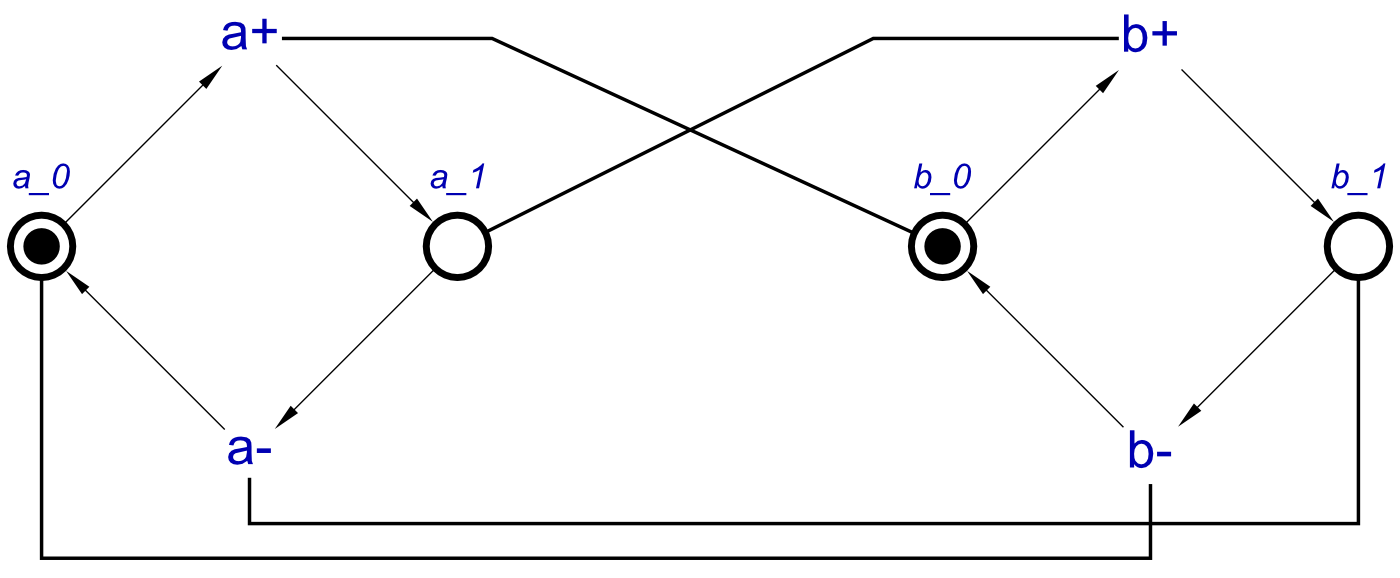
This will produce the following STG: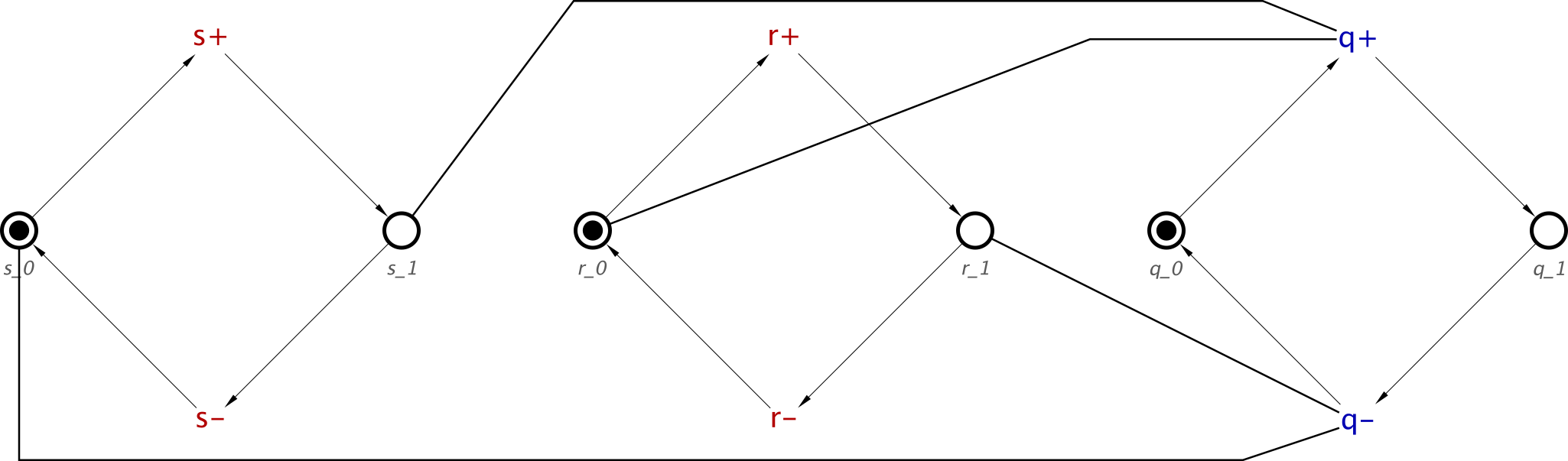STG_SR_Lath2

Changing the names of the signals does not affect the operation.

Now the SR-Latch has been defined, if a user has signals which will be inputs to a latch, they can use the concept and pass their signals into this, in the order of s, r and q.  For example someone can use the concept:

SRLatch(x, y, z)

In this case, x will be the set signal, y is the reset and z will be the output.

Some reuse

As is usually the case with concepts, we can define a SR-Latch using previously defined gates as concepts.

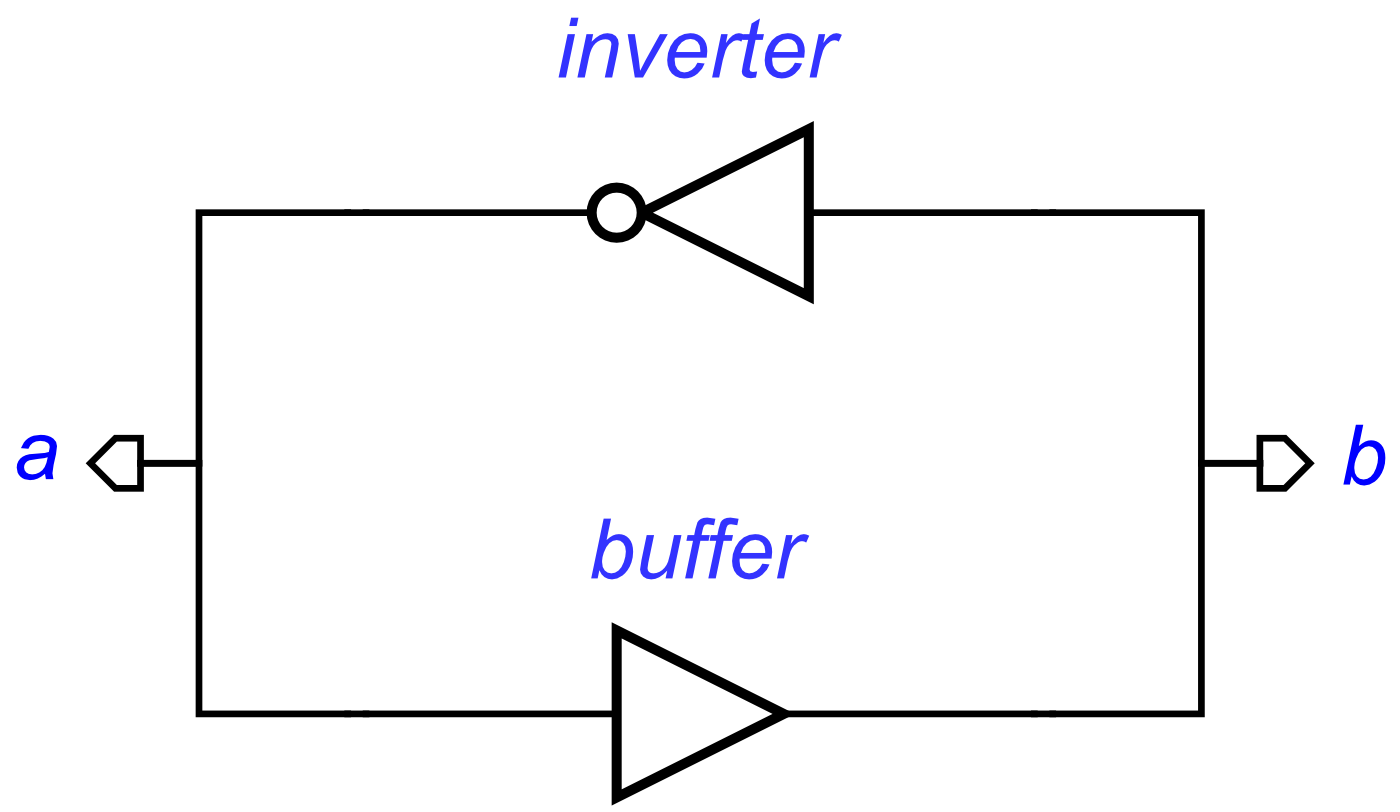
First of all, if we look at the set concept, it is clear that s and q form a buffer. So this can be rewritten as:

set = buffer(s, q)

The reset concept can also be redefined. In this case, it acts as an inverter:

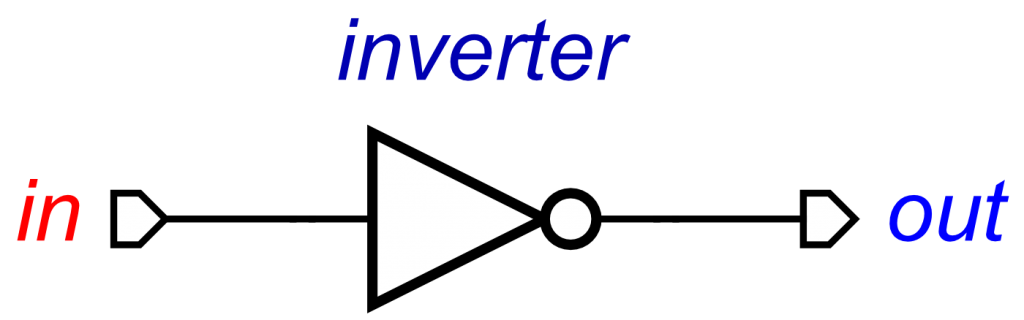
reset = inverter(r, q)

As the initial state doesn’t need to be changed, we can compose these concepts as above to produce the SRLatch concept:

SRLatch = set ⋄ reset ⋄ initialState

Or we can reduce the number of concepts defined and compose these as follows:

SRLatch = buffer(s, q) ⋄ inverter(r, q) ⋄ initialState

There are of course several ways of specifying an SRLatch using concepts, but these are two of the simpler ways, either using signal-level concepts, or predefined gate-level concepts. The preference is entirely on the user.

Finally

In this post, we have explained another simple logic gate. The discussion includes the basic operation being specified as signal-level concepts, or by taking this a step higher and using pre-defined gates.

We have also shown how while the concept defines certain signal names, these aren’t set. A default SRLatch concept will use these signal names, but if these signals are not used in a design, a user can pass the desired signal names into the concept, and these names will replace the default ones.

This blog series will continue soon, with the inclusion of further logic gates and how they can be defined simply.

Asynchronous, Buffer, Concepts, Inverter

Concepts III: Initial States

Leave a comment

Initial States

Now we have introduced a couple of simple gates, a buffer and an inverter, we should now discuss an important part of Signal Transition Graphs, and their implementation using Concepts. These are initial states.  

Initial states are used in Signal Transition Graphs to show what state a signal is in, high or low, when the system being designed starts. This is important as STGs require initial states for simulation, verification and synthesis.

In the previous posts, we have assumed that all signals involved in the STGs are initially set to 0, and this has been indicated by placing a token in the places which are before each signals + transition (as above), but this assumption cannot be applied to every STG.

Example – A Handshake

So now let’s use a previous example, a Handshake, and discuss what we can do to ensure there are initial states in an STG produced using concepts.

The concept used to describe a handshake is as follows:

handshake(a,b) = buffer(a,b) ⋄ inverter(b,a)

This concept captures the interactions of signals a and b, using previously defined buffer and inverter concepts, but this does not explain the state of these signals when the handshake starts.

Initial state concepts can be defined similarly to other concepts, and thus can be composed with other concepts as normal. For this example, let’s say the two signals involved in handshake are both initially 0.

initialState = initialise(a,0) ⋄ initialise(b,0)

There is some syntax to discuss here:

initialise(a,0) – This is used to express an initial state. The state of the signal, a, will be initially set to 0.

The concept, initialState, implies that the initial state of signals a and b will be 0, so the first transition of each can be +, from low to high.

Now we can include this concept with the handshake concept:

system = handshake(a,b) ⋄ initialState

Passing this concept into the algorithm will produce the same STG as in the previous post:

bufferAndInverter00

And this can be resynthesized to produce the same handshake STG:

handshake00

However, what if the initial states are not both 0? For this, let’s redefine the initial state concept and compose this with a handshake concept:

initialState = initial(a,0) ⋄ initial(b,1)
system = handshake(a,b) ⋄ initialState

Now, a should initially be 0, and b should initialy be 1. The STG produced from these concepts is:

BufferAndInverter01This is the same as the previous version, but the tokens have shifted. After resynthesis, the STG is as follows:BufferAndInvertorRe01Again, very similar to the previous post-resynthesis STG. But in this case, we can see that b- is the first transition, instead of a+.

No initial state concepts

So, what if a set of concepts doesn’t contain any initial state concepts. In this case, the STG produced may still be a correct implementation of the system, but a user may wish to do some testing with options for initial states open.

When this occurs, the algorithm has the option of adding some extra transitions to allow a user some options. So, for example, let’s define a handshake, but no initial states:

system = handshake(a,b)

In this case, we make no assumptions of initial states, but how does this affect the STG produced?

BufferInverterNoInit

The STG produced is very similar to the previous STG, the concepts used to describe which features initial states. In this case however, the places a_0, a_1, b_0 and b_1 are all free from tokens. In order to select an initial state, the algorithm adds in an extra place and two extra transitions per signal, in order to allow  a choice of each signal’s initial state.

Using this example, when a user starts the simulation, the first transitions to be enabled will be the transitions either high or low from the initial state selections, allowing the user to select a- to set this signal to 0 initially, or a+ to set it to 1 initially, and this is the same as with signal b.

After this choice is made, the initial state selection will no longer be usable until the simulation is started again. The user can test how the system runs using these initial states, and then restart to test another combination of initial states. After the initial states have been selected, the user can either change this STG, removing the initial state selections and adding tokens into the correct place, or they can add the initial states to the list of concepts, and re-compose these for a new STG.

DISCLAIMER – An STG featuring initial state selection is not a correct STG, it violates properties of STGs which are necessary in order to be used with tools which perform useful functions like synthesis, for example. Currently, this method of testing for initial states should be used only for simulation, to test how differing initial states can affect a system. Any future developments are made on how to include a choice  of initial state in a correct STG, a follow-up post will be made.

Finally

In this and the previous two posts, we have covered the basics of concepts, and the design process of various simple gates.  Now we can move onto discussing some more complicated designs, and how we can use pre-existing concepts, and define new ones.

The next blog post will be Concepts IV: A C-element. This will be the first in a set of posts describing some standard logic gates, and from this we will work up to some more complex examples, using some of the previously described gates.

Asynchronous, Concepts, Inverter, Logic Gate

Concepts II: An inverter

Leave a comment

An inverter

In the second post in the Concepts series we will discuss another simple logic gate, an inverter.

inverter

An inverter takes an input signal, and outputs a signal in the opposite, or inverted, state as the input signal, the output is simply the opposite of the input. For example, if the input signal changes from 0 to 1, the output will eventually change from 1 to 0. Similar to with the buffer, and the same with all gates, we say the output changes ‘eventually’ because the output changes after some unknown delay.

So how do we design an inverter using concepts? We need to describe what causes the output to transition, in terms of when the input transitions.  This can be described as:

inverter(in, out) = in+ ⇝ out- ⋄ in- ⇝ out+

This is very similar to the buffer concept, but with some subtle differences.  This concept implies that in+ causes out-.  This is composed with in- causing out+.  Therefore, this concept suggest that when the input transitions one way, the output will eventually transition in the opposite direction, for example, when in+ occurs, out- will eventually occur after, providing in stays high.

As with the previous post, we need to produce an STG from the inverter concept, which we can simulate, verify and test.  To do this, we pass this into the conversion algorithm, which starts as follows:

Buffer0

As with the buffer, it starts off by placing cycles for each individual signal.  This keeps the property of consistency in the STG, as discussed in Concepts I.

inverter1

Next, the first causality of the inverter concept is applied to these cycles.  This is in+ ⇝ out-. This connects the place after in+, labelled as in_1, with the signal transition of out-, using a read-arc. This is so that for out- to occur, in must have already transitioned high, which is displayed by in_1 possessing a token. The read-arc stops out- from consuming the token in in_1 which would block in- from happening, but allows out- to occur.

inverterSTG2

Finally, another read arc is used which represents the concept of in- ⇝ out+, connecting in_0 place with the out+ transition. This conversion of a concept to an STG is now complete, and this correctly represents the operation of an inverter.

Note, as with the buffer STG, that in the above STGs we assume that all signals are initialised to 0.  In this case, it means that the output can initially transition high and will do eventually, due to the fact that in input is initially 0.

In a later blog post we will see how to use concepts to specify initial states of all signals in a compositional manner.

More reuse

We have now defined both an inverter and a buffer in these first two posts.  So lets use these together to show some reuse, and how these can be used together.

For this example, lets use a buffer and inverter loop.  It doesn’t necessarily have any real-world applications as these logic gates, but it’s a perfect example to show how concepts can be composed, and produces some interesting results.

bufferinverter

The signals shown in this diagram are simply used for viewing the outputs from the inverter and the buffer, but can be used as part of the concepts.

This circuit can be produced from the following concept:

bufferAndInverter = buffer(a,b) ⋄ inverter(b,a)

In this circuit, a is an input to the buffer, but the output from the inverter, and these are connected.  b is another signal connecting the output of the buffer to the input of the inverter.

As with the doubleBuffer example from the previous post, we could have described this using signal-level concepts, which would be a longer description that that of the one above. Since we have defined both an inverter and a buffer, we can simply reuse this definition in order to save time on describing concepts. The bufferAndInverter STG will be, assuming all signals are initially 0, as follows:

bufferAndInverterSTG

By following pairs of arcs, it is possible to see which are a cause of the buffer, and which are a cause of the inverter.  This STG can now be simulated, and does in fact act as expected from the circuit above.  When a+ occurs, b+ is enabled,  and after it transitions, this will cause a- to be enabled.  When a- has occurred, b- can then occur, after which a+ is enabled, and this completes the circuit.

This STG can be resynthesized, and the result is rather interesting:

handshake1

The resulting STG is in-fact the STG for a handshake protocol.  This means that what we have defined above, bufferAndInverter, is actually a handshake, described using a buffer and an inverter.  Therefore, let’s drop the current name, and re-define it using some parameters, so that any pair of signals can be handshaked.

handshake(a,b) = buffer(a,b) ⋄ inverter(b,a)

Handshakes are very useful for asynchronous systems, and having a concept defined for use at any time can make the design process much easier and quicker.

Finally

In this post, we have discussed how to describe a second logic gate, an inverter. We have described this in terms of concepts, and shown the conversion to produce an STG. We have also shown how a buffer and an inverter can be used in conjunction with one-another to produce a circuit, now that both have been pre-defined.

The next post, Concepts III: Initial States will use buffers and inverters as examples of how initial states can be defined using concepts, or in the case that initial states are not defined, how the conversion algorithm will apply options for initial states, so an STG produced can still be used for simulation.