Category Archives: Logic Gate

Asynchronous, Buffer, Concepts, Inverter, Latch, Logic Gate, Uncategorised

Concepts V: Set-Reset Latch

Leave a comment

Set-Reset Latch

After learning how a C-element can be produce with concepts, we can introduce other gates. In this case another fairly standard gate, a latch.

The operation of a latch is to hold a given value. There are several different types of latch, but in this case we will talk about a Set-Reset latch (SR Latch). This latch has two inputs, one will set the latch when high, causing its one output to be high. The second input will reset the latch when it is high, causing its output to be low.

So lets see how we can specify this using concepts.

Concepts

For this, let’s start off by referring to the two inputs as a and b. The output is c.

So, first of all, lets think about how we can set the latch:

set = a+ ⇝ c+ ⋄ a- ⇝ c-

And it’s that simple. Simply put, when one of the outputs, a in this case, goes high, we want the output, c, to go high.

So we have described the interaction for set using one of the inputs and the output, now lets describe the reset action:

reset = b+ ⇝ c- ⋄ b- ⇝ c+

This will cause the output to go low when the second input, b, goes high.

These two concepts describe the operation of a SR-latch. But we still need to think about how the SR-latch will act initially, such as when it first receives power.

Unless specifically required, we should assume that the output of the latch should be low at startup. Because of this, we don’t want it to be set initially by a being high, so we can set this to 0 initially also.

However, with the second input, b, setting this high at this point would ensure that the output will reset to 0 at start up, but if the initial state of c is already set to low initially, we shouldn’t need to set b to high, so we will set the initial state of this to low too.

The initial state concept will be as follows:

initialState = initialise(a, 0) ⋄ initialise(b, 0) ⋄ initialise(c, 0)

Now let’s create the scenario concept for the SR-Latch:

SRLatch = set ⋄ reset ⋄ initialState

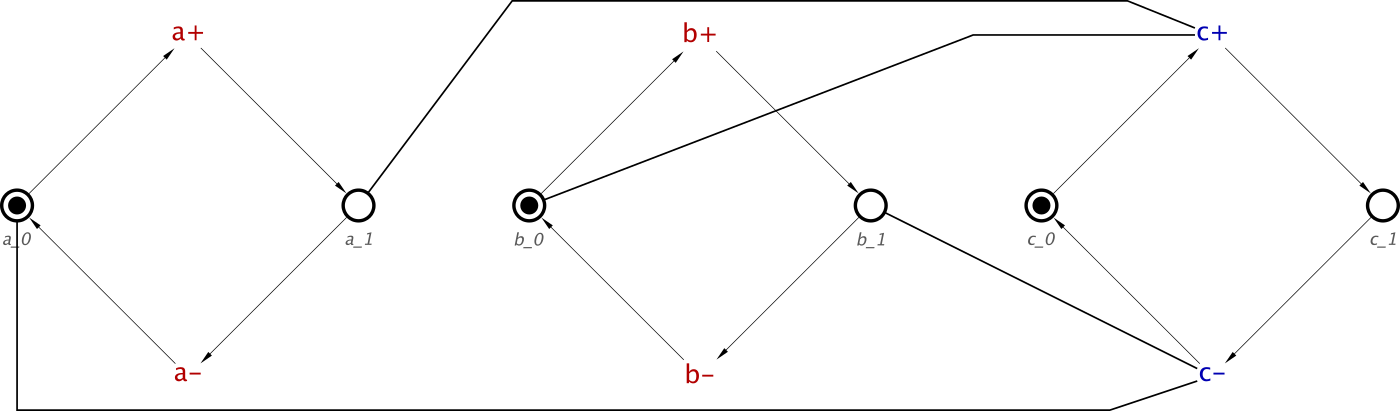
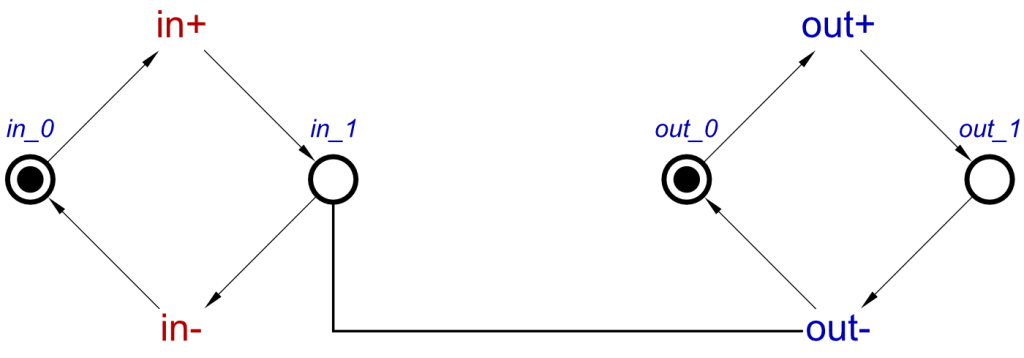
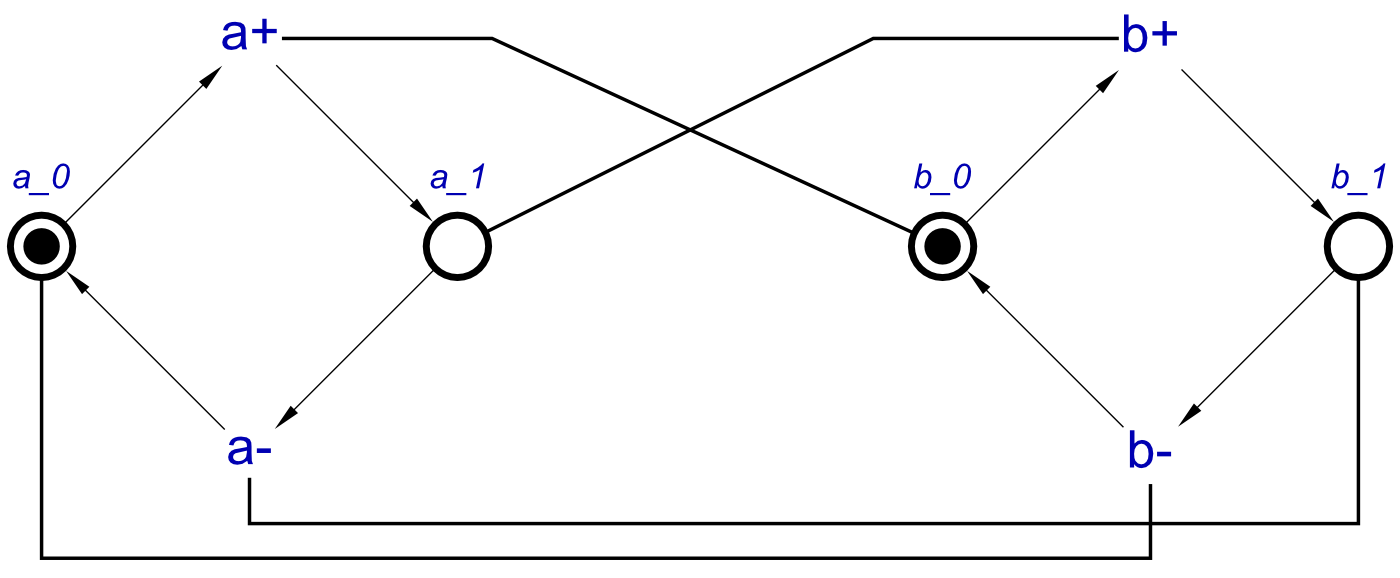
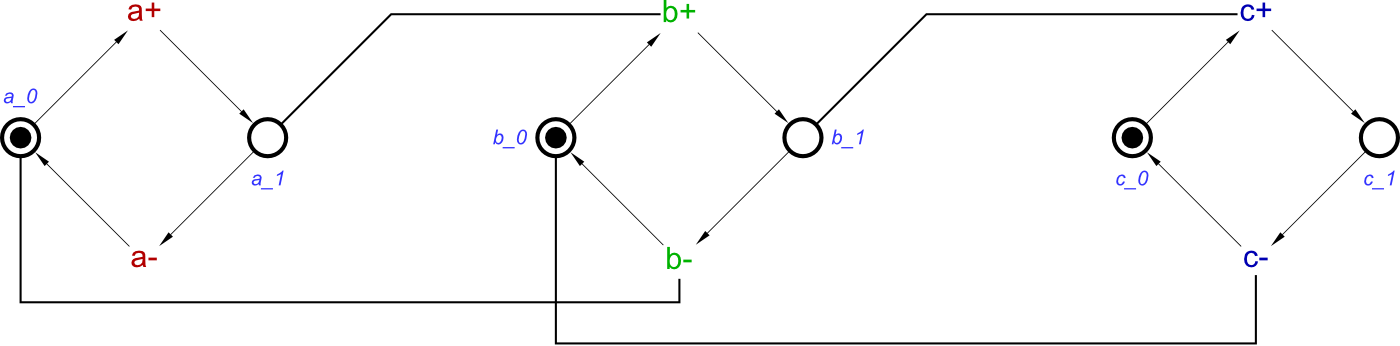
And this can be converted to a Signal Transition Graph, so this specification can be verified, simulated, tested and then synthesised. The STG for a SRLatch will be as follows:

STG_SR_Latch

This is a fairly simple STG, but simulation would prove that setting a high will allow c to transition high. Once it has transitioned high, it cannot transition low until b has been set high.

For some simpler understanding of how this latch works, we can change some of the signal names. In this case, we will change a to s, which stands for set. b will be set to r, which stands for reset. Finally, we can call c, q. q is a standard output symbol for latches.

This will change the concepts to the following:

set = s+ ⇝ q+ ⋄ s- ⇝ q-
reset = r+ ⇝ q- ⋄ r- ⇝ q+
initialState = initialise(s, 0) ⋄ initialise(r, 0) ⋄ initialise(q, 0)
SRLatch = set ⋄ reset ⋄ initialState

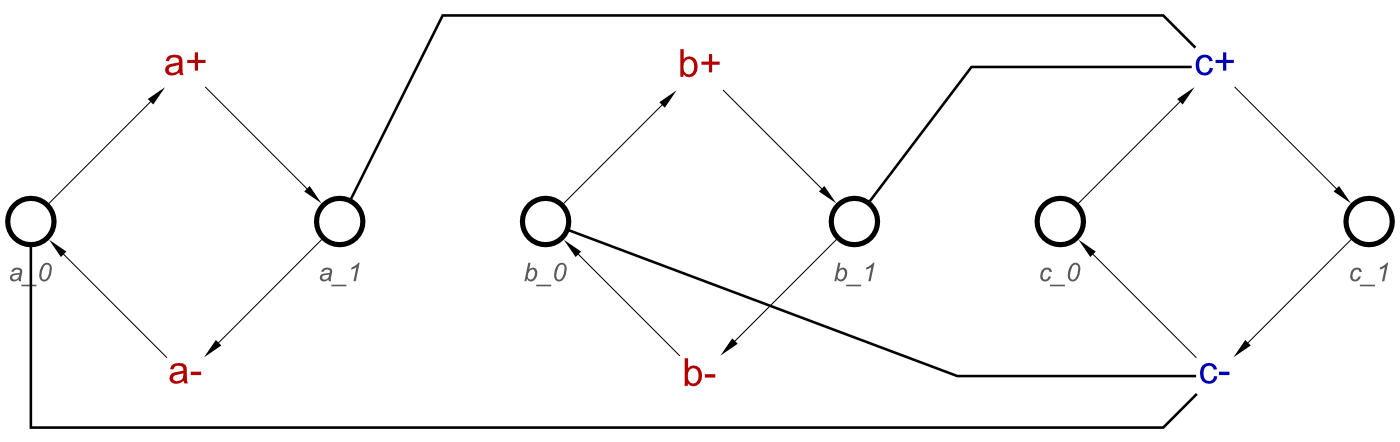
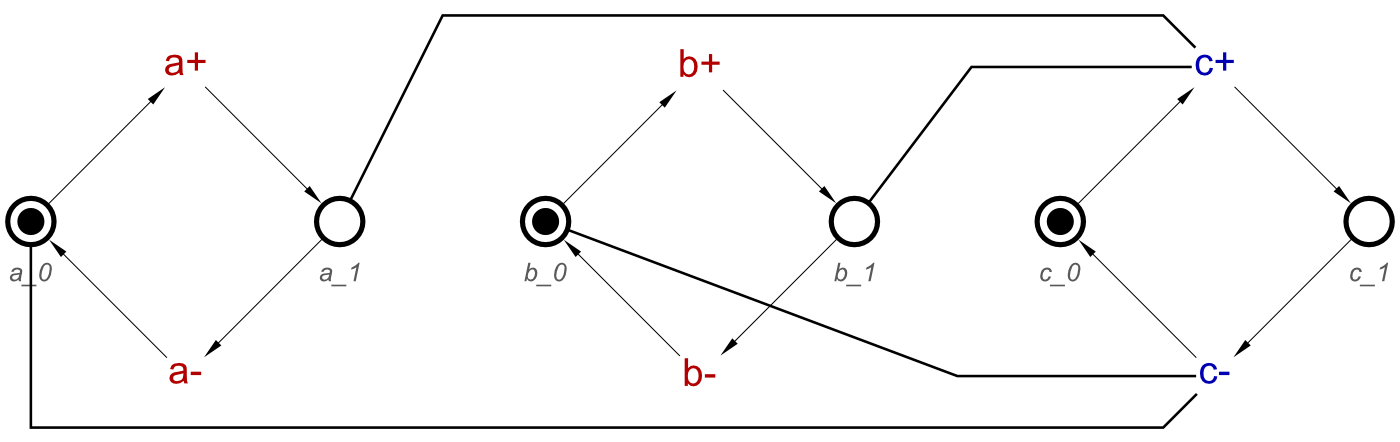
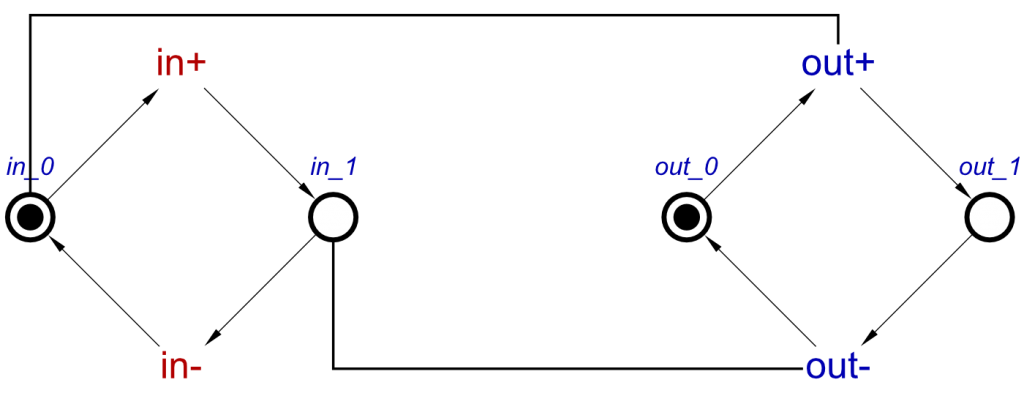
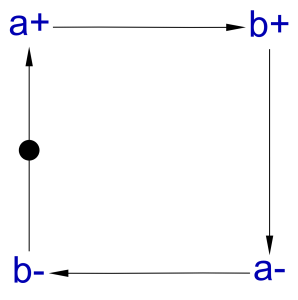
This will produce the following STG: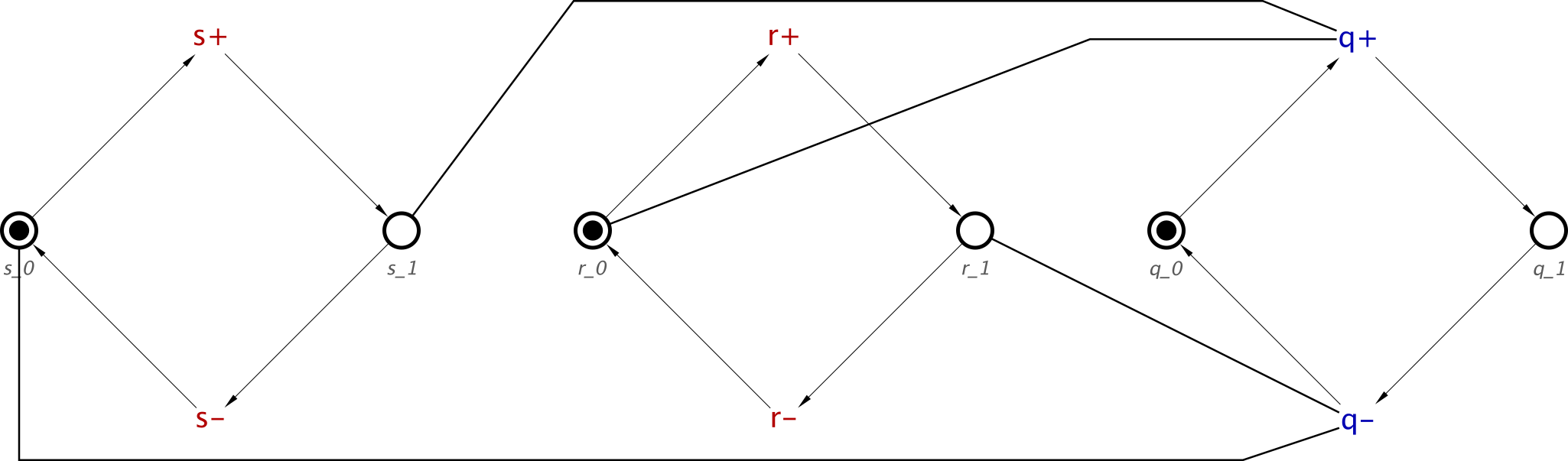STG_SR_Lath2

Changing the names of the signals does not affect the operation.

Now the SR-Latch has been defined, if a user has signals which will be inputs to a latch, they can use the concept and pass their signals into this, in the order of s, r and q.  For example someone can use the concept:

SRLatch(x, y, z)

In this case, x will be the set signal, y is the reset and z will be the output.

Some reuse

As is usually the case with concepts, we can define a SR-Latch using previously defined gates as concepts.

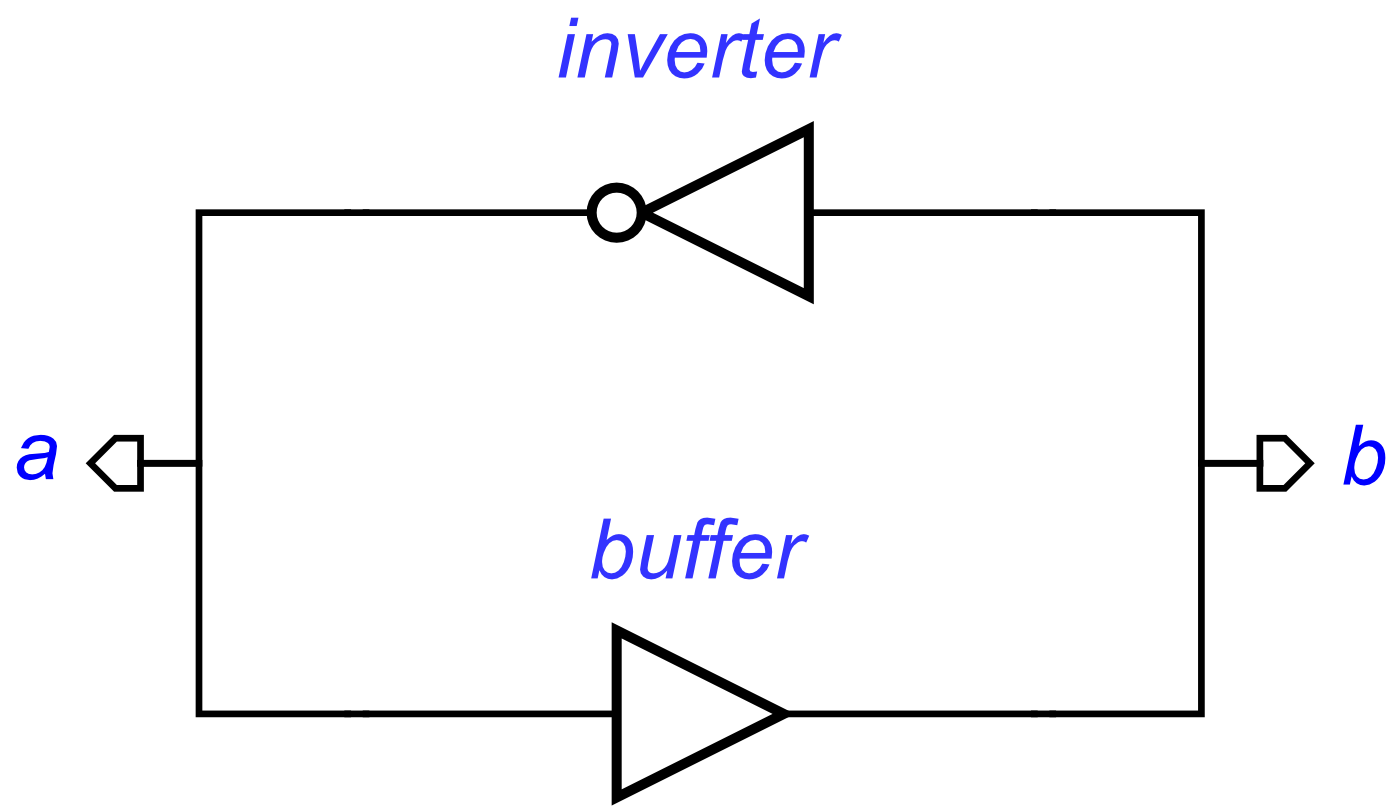
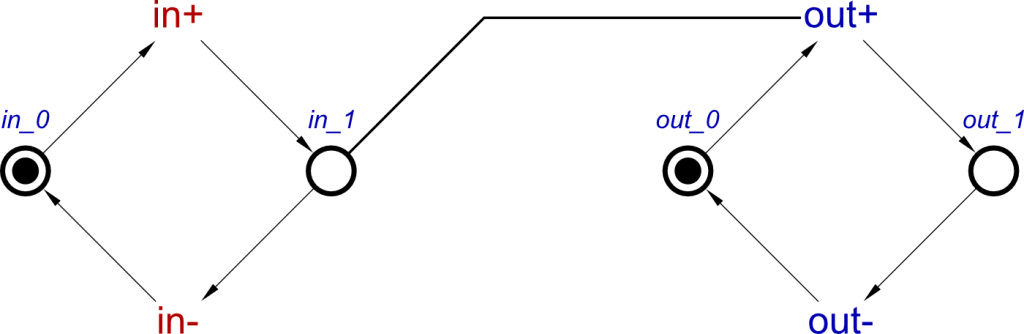
First of all, if we look at the set concept, it is clear that s and q form a buffer. So this can be rewritten as:

set = buffer(s, q)

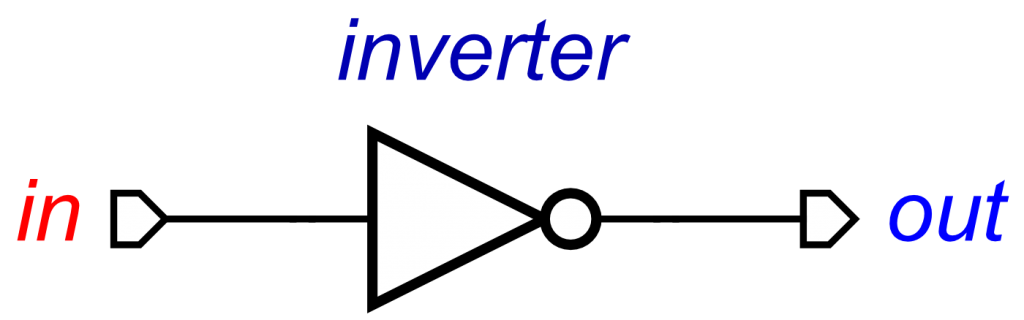
The reset concept can also be redefined. In this case, it acts as an inverter:

reset = inverter(r, q)

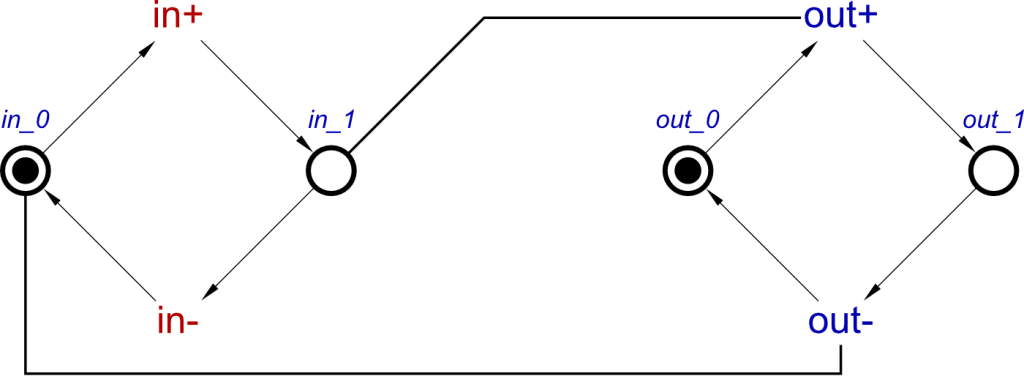
As the initial state doesn’t need to be changed, we can compose these concepts as above to produce the SRLatch concept:

SRLatch = set ⋄ reset ⋄ initialState

Or we can reduce the number of concepts defined and compose these as follows:

SRLatch = buffer(s, q) ⋄ inverter(r, q) ⋄ initialState

There are of course several ways of specifying an SRLatch using concepts, but these are two of the simpler ways, either using signal-level concepts, or predefined gate-level concepts. The preference is entirely on the user.

Finally

In this post, we have explained another simple logic gate. The discussion includes the basic operation being specified as signal-level concepts, or by taking this a step higher and using pre-defined gates.

We have also shown how while the concept defines certain signal names, these aren’t set. A default SRLatch concept will use these signal names, but if these signals are not used in a design, a user can pass the desired signal names into the concept, and these names will replace the default ones.

This blog series will continue soon, with the inclusion of further logic gates and how they can be defined simply.

Asynchronous, CElement, Concepts, Logic Gate

Concepts IV: C-Element

Leave a comment

C-Element

Finally, after introducing the basics of concepts, we can now apply this to the design of logic gates. In this post, we will produce a very standard gate, a C-Element.

A C-Element’s basic operation is that, when all the inputs to the gate are high, or 1, then the output will be set high. This output will remain high until all of the inputs are low, or 0, at which point the output will be set low.

So let’s describe this using concepts!

Concepts

For this example, the C-Element we describe will be a 2 input gate. These will be a and b.  The single output will be c. 

So let’s start with describing what causes the output to go high:

outputRise =  a+ ⇝ c+ ⋄ b+ ⇝ c+

This concept will cause the output, c, to go high when both the inputs, a and b, are high.

Next, let’s describe what causes the output to go low:

outputFall =  a- ⇝ c- ⋄ b- ⇝ c-

Similar to the previous concept, outputFall will cause c to go low only when both a and b are low.

And these two concepts describe the operation of a C-element. Let’s combine them, and then we can Convert them to an STG, giving us the following:

C-Element = outputRise ⋄ outputFall

C-Element1

In this state however, this STG is not particularly useful, as there are no initial states, and therefore it cannot be simulated or synthesized. Thus, let’s add an initial state concept:

initialState = initialise(a, 0) ⋄ initialise(b, 0) ⋄ initialise(c, 0)
CElement  = outputRise ⋄ outputFall ⋄ initialState

By setting all the initial states to 0, we can then test this STG using Workcraft, and see that the STG (shown below) operates as a C-element.

C-Element2

This STG could also be tested by setting the initial states to any combination. The C-Element would still act as expected.

Some reuse

It is possible to describe a C-Element using predefined gates. If we break down some of the concepts used above we find some interesting points.

If we take the interactions of just one input signal and the output signal from the above concepts we get the following:

input1 = a+ ⇝ c+ ⋄ a- ⇝ c-

This concept is actually exactly the same as a gate we have previously defined: a buffer. Thus, a C-Element can actually be described using these:

CElement = buffer(a, b) ⋄ buffer(b, c) ⋄ initialState

The initial state must be included in order for the resulting STG to be usable in further operations.

Finally

This blog post has finally explained how concepts can be used to design a logic gate, albeit a simple one. This includes describing it’s operations in terms of the interactions of the input and output signals, or using predefined concepts, particularly a buffer.

The next post will continue in the effort to define logic gates using behavioural concepts, the next being an Set-Reset Latch. 

Asynchronous, Concepts, Inverter, Logic Gate

Concepts II: An inverter

Leave a comment

An inverter

In the second post in the Concepts series we will discuss another simple logic gate, an inverter.

inverter

An inverter takes an input signal, and outputs a signal in the opposite, or inverted, state as the input signal, the output is simply the opposite of the input. For example, if the input signal changes from 0 to 1, the output will eventually change from 1 to 0. Similar to with the buffer, and the same with all gates, we say the output changes ‘eventually’ because the output changes after some unknown delay.

So how do we design an inverter using concepts? We need to describe what causes the output to transition, in terms of when the input transitions.  This can be described as:

inverter(in, out) = in+ ⇝ out- ⋄ in- ⇝ out+

This is very similar to the buffer concept, but with some subtle differences.  This concept implies that in+ causes out-.  This is composed with in- causing out+.  Therefore, this concept suggest that when the input transitions one way, the output will eventually transition in the opposite direction, for example, when in+ occurs, out- will eventually occur after, providing in stays high.

As with the previous post, we need to produce an STG from the inverter concept, which we can simulate, verify and test.  To do this, we pass this into the conversion algorithm, which starts as follows:

Buffer0

As with the buffer, it starts off by placing cycles for each individual signal.  This keeps the property of consistency in the STG, as discussed in Concepts I.

inverter1

Next, the first causality of the inverter concept is applied to these cycles.  This is in+ ⇝ out-. This connects the place after in+, labelled as in_1, with the signal transition of out-, using a read-arc. This is so that for out- to occur, in must have already transitioned high, which is displayed by in_1 possessing a token. The read-arc stops out- from consuming the token in in_1 which would block in- from happening, but allows out- to occur.

inverterSTG2

Finally, another read arc is used which represents the concept of in- ⇝ out+, connecting in_0 place with the out+ transition. This conversion of a concept to an STG is now complete, and this correctly represents the operation of an inverter.

Note, as with the buffer STG, that in the above STGs we assume that all signals are initialised to 0.  In this case, it means that the output can initially transition high and will do eventually, due to the fact that in input is initially 0.

In a later blog post we will see how to use concepts to specify initial states of all signals in a compositional manner.

More reuse

We have now defined both an inverter and a buffer in these first two posts.  So lets use these together to show some reuse, and how these can be used together.

For this example, lets use a buffer and inverter loop.  It doesn’t necessarily have any real-world applications as these logic gates, but it’s a perfect example to show how concepts can be composed, and produces some interesting results.

bufferinverter

The signals shown in this diagram are simply used for viewing the outputs from the inverter and the buffer, but can be used as part of the concepts.

This circuit can be produced from the following concept:

bufferAndInverter = buffer(a,b) ⋄ inverter(b,a)

In this circuit, a is an input to the buffer, but the output from the inverter, and these are connected.  b is another signal connecting the output of the buffer to the input of the inverter.

As with the doubleBuffer example from the previous post, we could have described this using signal-level concepts, which would be a longer description that that of the one above. Since we have defined both an inverter and a buffer, we can simply reuse this definition in order to save time on describing concepts. The bufferAndInverter STG will be, assuming all signals are initially 0, as follows:

bufferAndInverterSTG

By following pairs of arcs, it is possible to see which are a cause of the buffer, and which are a cause of the inverter.  This STG can now be simulated, and does in fact act as expected from the circuit above.  When a+ occurs, b+ is enabled,  and after it transitions, this will cause a- to be enabled.  When a- has occurred, b- can then occur, after which a+ is enabled, and this completes the circuit.

This STG can be resynthesized, and the result is rather interesting:

handshake1

The resulting STG is in-fact the STG for a handshake protocol.  This means that what we have defined above, bufferAndInverter, is actually a handshake, described using a buffer and an inverter.  Therefore, let’s drop the current name, and re-define it using some parameters, so that any pair of signals can be handshaked.

handshake(a,b) = buffer(a,b) ⋄ inverter(b,a)

Handshakes are very useful for asynchronous systems, and having a concept defined for use at any time can make the design process much easier and quicker.

Finally

In this post, we have discussed how to describe a second logic gate, an inverter. We have described this in terms of concepts, and shown the conversion to produce an STG. We have also shown how a buffer and an inverter can be used in conjunction with one-another to produce a circuit, now that both have been pre-defined.

The next post, Concepts III: Initial States will use buffers and inverters as examples of how initial states can be defined using concepts, or in the case that initial states are not defined, how the conversion algorithm will apply options for initial states, so an STG produced can still be used for simulation.

Asynchronous, Buffer, Concepts, Logic Gate

Concepts I: A buffer

Leave a comment

A Buffer

In this post, we will discuss one of the most simple logic gates, a buffer.

buffer_schematic

A buffer takes an input signal, and outputs a signal in the same state as the input signal, the output simply follows the input. For example, if the input signal changes from 0 to 1, the output will eventually change from 0 to 1. We say the output changes ‘eventually’ because the output changes after some unknown delay. It is possible for the input to change from 0 to 1, and then back to 0 very quickly, before we see any changes on the output. But intuitively, we want to be able to say that if the input transitions from 0 to 1, then stays 1 long enough, the output will follow and also transition to 1.

So how can we design these using concepts? We need to describe the causal relationship between the input and output; what occurs in the input to cause a transition in the output? For a buffer, this is when a signal transition occurs on the input, this needs to be reflected on the output.  This can be described as:

buffer(in, out) = in+ ⇝ out+ ⋄ in- ⇝ out-

There are some operators to discuss here:

⇝ – Shows the causal relationship
⋄  – The composition operator

This concept therefore implies that in+ causes out+, this is composed with in- causing out-.  This covers all the operations of the buffer.

But now, how does this turn into a Signal Transition Graph, which we can simulate, verify and test to ensure it works correctly? This is performed using an algorithm:

Buffer0

First of all, the algorithm takes the list of concepts and finds places one of these cycle for each individual signal. This is to keep with the property of consistency, where positive (+) and negative (–) transitions of each signal must always alternate. This is also in-keeping with the possibility for a signal to transition one way and back quickly without affecting the others, as with the example of the input transitioning high and then low before the output changes.

buffer1

Next, the algorithm uses the first concept, in+ ⇝ out+, to show this causality in the STG. This concept shows how the input rising causes the output to rise, so this is viewed in an STG by connecting the in_1 place, which shows when the input has transitioned high, to the transition of out+. This is done using an arc commonly known as a read-arc. This is because a one way arc connecting these STG components would mean that when out+ occurs, a token in in_1 is consumed, blocking in- from being enabled. A read-arc allows out+ to simply check for a token in in_1 for it to occur without consuming it.

Buffer2

In the final step for designing a buffer, another read arc is used which represents the concept of in- ⇝ out-, connecting in_0 place with the out- transition. This conversion of a concept to an STG is now complete.

Note that in the above STGs we assume that all signals are initialised to 0.  In a later blog post we will see how to use concepts to specify initial states of all signals in a compositional manner.

Reuse

Now we have defined a buffer, we can reuse this. As said earlier in this post, a concept can be defined as several concepts. Therefore, let use an example of a circuit which uses buffers.

double_buffer_schematic

This circuit can be produced from the following concept:

doubleBuffer = buffer(a,b) ⋄ buffer(b,c)

In this circuit, a is an input, c is an output, and b is an internal signal connecting the output of buffer_1 to the input of buffer_2. We could have described this using signal-level concepts, which would be a longer description that that of the one above. Since we have defined a buffer, we can simply reuse this definition in order to save time on describing concepts. This produces the following Signal Transition Graph:

doubleBufferSTG

Comparing this STG to the STG for a single buffer, it is possible to see that a and b in this STG form one buffer, and b and c form another buffer.  Again, we assume that all signals are initially 0.

Finally

In this first blog post, we have discussed how to describe a simple logic gate, a buffer, in terms of concepts. How these concepts are then converted into a Signal Transition Graph is also described. Another useful aspect of concepts is their reusability, and how a defined concept can be reused is displayed in an example using two buffers.

The following post, Concepts II: An inverter will discuss another simple logic gate, an inverter. After having defined these two gates, a further post will explain how initial states work, whether defined as part of a concept or not, using both a buffer and an inverter as examples.