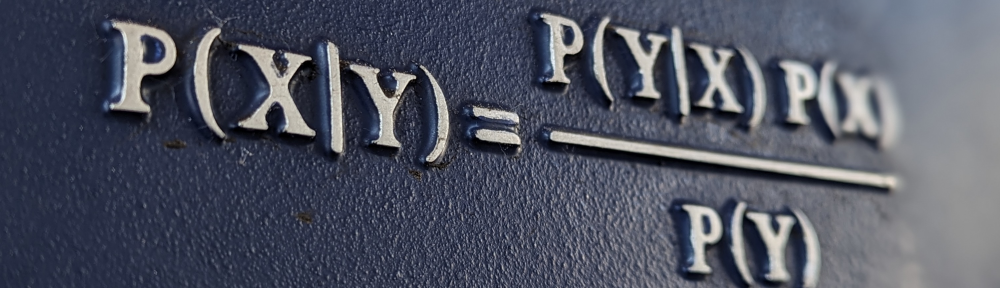Studentship code: MSP107

Abstract:

Gradient flows provide a powerful mathematical framework for describing how probability distributions evolve over time, forming the theoretical backbone of many modern machine learning algorithms. Methods such as Stein Variational Gradient Descent (SVGD), Langevin dynamics, and optimal transport-based samplers can all be viewed as discretised approximations of continuous-time gradient flows. However, these discretisations introduce design choices—step sizes, update rules, noise levels, transport maps—that strongly influence the quality, efficiency, and stability of the resulting algorithms.

Reinforcement Learning (RL) offers a compelling solution by framing optimisation as a sequential decision-making problem. Rather than relying on static heuristics, an RL agent can learn adaptive strategies to maximise long-term performance. While RL has revolutionised control and robotics, its potential to automate and accelerate probabilistic inference remains largely untapped.

This PhD project will explore the emerging interface between gradient flows and RL. The central idea is to treat the evolution of a gradient flow as a controllable dynamical system, and to use RL to learn optimal update rules, transport maps, or proposal distributions. This perspective has the potential to unlock several new research directions:

• RL-enhanced MCMC: learning state-dependent proposals that adaptively steer Markov chains towards efficient mixing.
• Adaptive inference algorithms: designing RL-driven controls that minimise asymptotic variance or maximise effective sample size.
• Optimising variational transport: using RL to learn optimal transport maps for Bayesian inference and generative modelling.
• Data-driven discretisations: discovering new numerical schemes for gradient flows tailored to specific applications.

The project is ideal for students interested in machine learning theory, probabilistic modelling, optimal transport, or reinforcement learning. It offers a unique opportunity to contribute to a fast-growing research area that combines rich mathematical structure with cutting-edge computational methods.

The successful candidate will gain experience in stochastic processes, numerical analysis, RL algorithms, and modern ML frameworks, and will have considerable freedom to develop their own theoretical and applied directions within this exciting new paradigm.

Studentship code: MSP108

Abstract:

For runners in long-distance races such as marathons, accurately predicting the finishing time is crucial for selecting the pacing strategy which leads to the best possible performance: Run too fast and you will “hit the wall”. Run too slow and you won’t reach your full potential. Similar considerations apply in other endurance sports, e.g., cycling or rowing, or even in non-sports contexts such as in the military.

Conventional approaches for finishing-time prediction are static, i.e., they only make predictions before the race. Once the race has started, they can neither account for an over-optimistically chosen initial pace nor adapt to unexpected factors affecting performance. A small number of dynamic approaches exist in the literature but these are often based on mathematical models which are too simplistic.

This project aims to predict the finish time combined with a systematic quantification of uncertainty and to update the prediction in real time as new data come in. To that end, you will develop dynamic Bayesian models which make use of some of the data collected by fitness trackers/GPS watches during a race, e.g. pace, heart-rate or elevation data, along with other covariates. You will also develop suitable computational statistical methods (e.g. based around sequential Monte Carlo methods) which can be used to update the prediction as new data become available throughout the race.

Studentship code: MSP109

Abstract:

The latent ancestral tree connecting a collection of DNA sequences is a central object of interest in statistical phylogenetics. There are well-established stochastic models for these latent trees based on coalescent and branching processes, but sampling from the posterior distribution of trees given observed DNA sequence data under these models remains a challenging problem. The space of trees is not even a vector space, so that most rules-of-thumb for designing effective MCMC proposals are difficult to apply. Trees are also large objects to store and manipulate in memory, which further impedes the practicality of algorithms.

Recent work has introduced a remarkably efficient data structure for storing a correlated sequence of trees [1, 5]. To date, the structure has been exploited for simulation, storage, and inference of so-called recombining genomes, whose ancestral tree varies along the genome. This project is about investigating what the same tree sequence data structure can contribute to tree-valued MCMC, where storage of many trees which build up differences gradually is equally important. Being able to store a full tree-valued MCMC run will increase the efficiency of algorithms in its own right, and also make it possible to investigate follow-up questions on postprocessing, such as optimal thinning [3], the design of control variates [4], or adapting the underlying stochastic model itself to facilitate computational scalability [2].

This project combines stochastic processes and modelling with computational statistics and software development. The balance of those elements can be adjusted to suit the interests of the successful applicant, but a willingness to engage with all three aspects is essential.

[1] Baumdicker et al. (2022). Efficient ancestry and mutation simulation with msprime 1.0. Genetics 220(3):iyab229.
[2] Bisschop, Kelleher and Ralph. Likelihoods for a general class of ARGs under the SMC. Genetics, iyaf103.
[3] Riabiz et al. (2022). Optimal Thinning of MCMC Output. J. R. Stat. Soc. B 84(4):1059-1081.
[4] South and Sutton (2025). Control variates for MCMC. arXiv:2402.07349.
[5] Wong et al. (2024). A general and efficient representation of ancestral recombination graphs. Genetics 228(1):iyae100.

Studentship code: MSP110

Abstract:

Markov Chain Monte Carlo (MCMC) methods are powerful tools for generating samples from complex probability distributions. They are central to many modern scientific fields, including Bayesian statistics, cosmology, molecular dynamics, and machine learning. Yet traditional MCMC methods can struggle in demanding settings—such as rare-event problems, multi-modal distributions with multiple separated peaks, or very high-dimensional spaces.

This PhD project will study modern MCMC algorithms that aim to address some of these challenges. The work will involve a combination of theoretical investigation, numerical exploration, and applied case studies. A key theme is the use of continuous-time processes with adjustable “speed” (also known as time-change) to improve how efficiently the algorithm explores the underlying space.

The direction of the project can be adapted to the student’s background and interests, whether they lean more towards theory, computation, or applications.

Some of these ideas are explored in the following papers:

• Section 4.2.2 of https://arxiv.org/pdf/2511.21563
• https://projecteuclid.org/journals/annals-of-applied-probability/volume-33/issue-6A/Speed-up-Zig-Zag/10.1214/23-AAP1930.full
• https://arxiv.org/pdf/2501.15155

Some of these ideas are also explored in the following video: https://www.youtube.com/watch?v=suzXZ5YPq74

Studentship code: MSP111

Abstract:

Extreme events play a central role in modern risk management and financial decision-making, where rare but catastrophic losses can propagate across markets, sectors, and entire economic systems. This phenomena, including market crashes, systemic failures, and large portfolio drawdown usually exhibit heavy-tailed behaviour, meaning that extreme observations occur with non negligible probability.

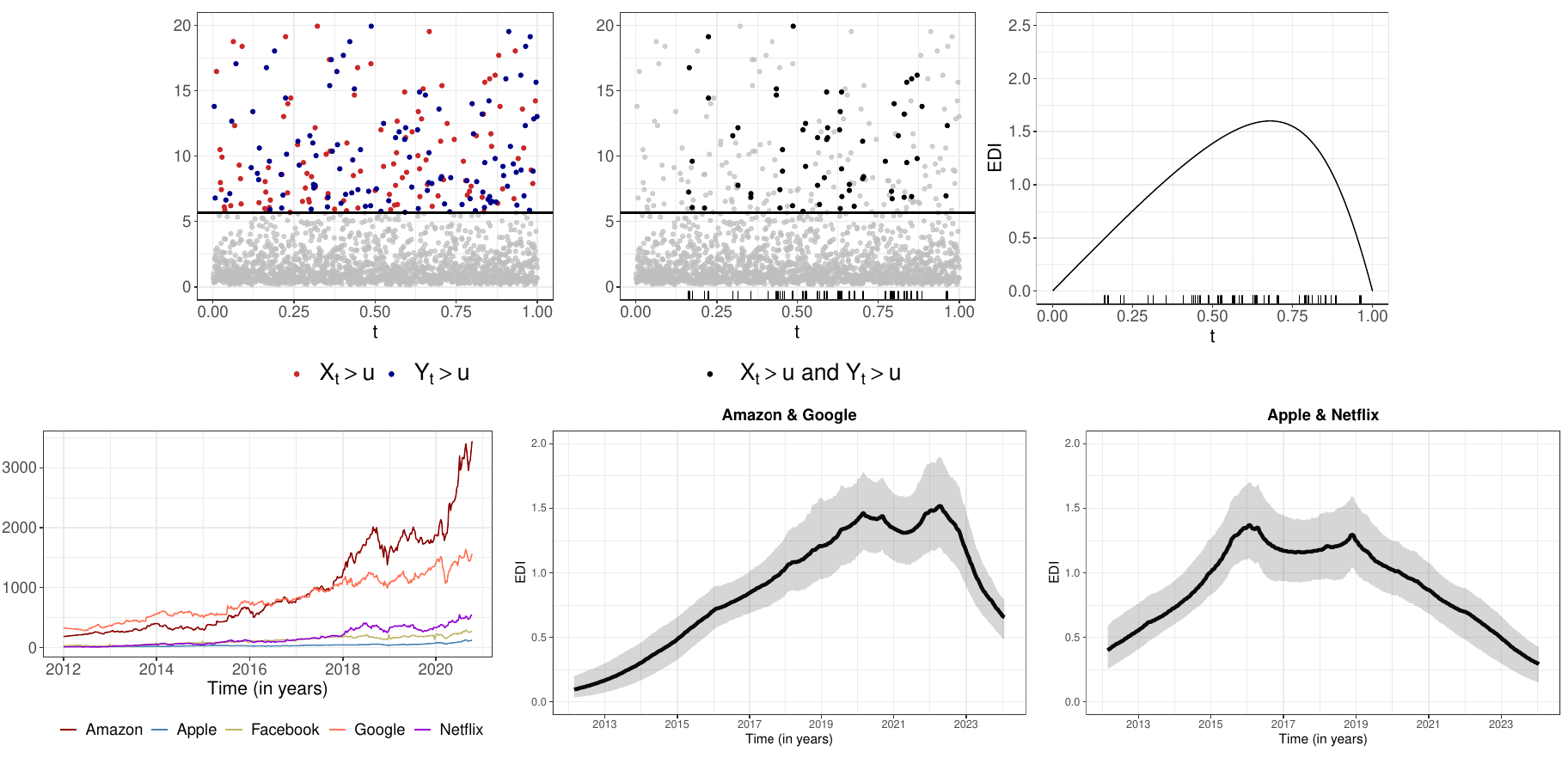
Extreme financial losses often cluster and propagate across assets, creating complex dependence structures that traditional models struggle to capture. This PhD project aims to develop new statistical methodology for modelling extremal dependence in multivariate and portfolio settings, extending recent work in which we introduced the Extremal Dependence Intensity (EDI) (see [1]) to track the dynamics of joint tail losses.

Building on the EDI framework, the project will explore more general and flexible approaches to modelling multivariate and portfolio extremes, including methods that incorporate covariates or time-varying market conditions to better understand how extremal dependence evolves. The project sits at the interface of two areas: Extreme Value Theory and Bayesian Statistics. By combining the theoretical foundations of both fields, the aim is to develop new classes of heavy-tailed models and covariate-dependent priors tailored for tail inference with a focus on estimating the tail dependence, modelling joint exceedances, and capturing the behaviour of heavy-tailed risks in high-dimensional financial systems. Applications include understanding financial crisis, systemic risk analysis, and portfolio optimisation under extreme scenarios. The project blends theory, computation, and real-world financial data, aiming to deliver practical tools for understanding and managing joint extremes in modern risk management.

[1] de Carvalho, M. and Palacios Ramirez, K. V. (2025). Semiparametric Bayesian modelling of nonstationary joint extremes: How do big tech’s extreme losses behave?, Journal of the Royal Statistical Society Series C: Applied Statistics 74(2): 447–465.

Studentship code: MSP112

Abstract:

Genetics datasets may have millions of variables but generally only a few hundred will be associated with a particular disease. This is a ‘needle in a haystack’ problem where false positive associations can lead to expensive and time-consuming wasted research. The standard statistical methods applied to these kinds of data are therefore conservative and often quite simple statistically.

Bayesian Additive Regression Trees (BART) are an increasingly popular method at the intersection of statistics and machine learning. However, there has been limited exploration of their use in modelling large genetics datasets. This PhD project will build on initial work carried out as part of an EPSRC-funded grant on the application of BART to genome-wide association study data. The student will be involved in setting the scope of the project. Possibilities include development of more efficient MCMC samplers for exploring the tree space, or work on real genetics data with a more applied emphasis.