The debate continued – it has moved to the notion of momentum.

And we seem to start to find agreement on some points.

 

Alex:

Thank you. I can accept your reasoning for the sake of Natural Philosophy and possibly application to Newtonian Mechanics.

(there is an expression in English “for the birds” – what I don’t want is that all this is useless for what we can see in transmission lines and Catt Theory) 

So, let’s try to find some common ground. In fact I made my first attempt in my Royal Society paper, where I talked about your reasoning (I hope it wasn’t in contradiction with you) and how it may be applied to Electromag (note that I wasn’t specific about applying it to Catt Theory).

Basically, I am struggling in defining what momentum p is in terms of Catt. And I think this is what Ivor asked you his last email. 

For example, if you say that E and p are in the same place and at the same time in the transmission line, and they are in proportion of c, we can argue that, since c is sqrt of 1/mu*eps (where mu and eps are the characteristics of the space where we are interested in the presence of E and p), then, basically E and p are the characteristics of the Poynting vector value ExH in that place in space and time. Right?

I suppose that, then since Ivor used to say “Energy density = EH/c”  (where he wrote the vector product in shorthand, but basically he meant Energy density=ExH/c)

it looks like in your terms of E/c=p, we effectively say that p (momentum) is Energy density. Right?

So, this momentum propagates in transmission line together with ExH.

Now a more interesting stage of discourse:

You state that this momentum p (i.e. the “effect” of the Energy being “cause”) if it affects some finite mass it may ‘hit’ it with the effect of mv, right?

So, we can have the mechanical (or material ?) consequent of this effect in particles, (if) located next to the point of contact with them, so that these particles move (possibly, tangential to the plane of ExH?)  with velocity v. Right?

Let first agree on the above “Right’s?”, before we move further, OK?

Ed:

natural philosophy began in the 17^th century with Galileo and Newton as a geometrical theory of motion (description) and its generating cause (explanation).The aim was to understand how Nature really works. The basic insight was that the observable processes in Nature were generally such of motion, its generation, and its destruction. The common conviction was that “he who hasn’t understood motion, has not understood Nature” (Henry Oldenbourg, first secretary of the Royal Society, founded 1660). Galileo laid the foundation in his “Discorsi” (1638), beginning with a description of unresisted uniform straightline motion in space and time. He found that the motion of a body covering some space in consuming some time proceeded according to the geometrical law of equal integer multiples (Euclid),  the steps of space, ∆L, being proportional to the steps of time, ∆T, so that the relation of space to time was constant [L/T]. Here is Galileo’s diagram. JK is the standard of “time”, GH is the standard of “space”.

Note that every increment of space is proportional to the corresponding increment of time (AB/DE, BC/EF, etc.), so that the relation “space over time”, [L/T], is always constant, independently of the measure (length) of the increments. This constant parameter [L/T] characterizes the natural “space-time frame of reference” of motion given through the standards of time, JK, and space, GH. Space, time, and motion are discrete or quantized, being scaled standards, according to the Ancient “atomistic” view held by Galileo and Newton.

Galileo also investigated the “cause” of motion, starting with “change of” motion in the case of “acceleration” to be observed in the phenomena of free fall, using the “preferred” absolute space-time frame of reference just described. The result was that motion is generated stepwise by addition of finite increments ∆L, ∆T of space and time, and that the generating cause thereof is as a quantity preserved when a moving body’s direction changed from the vertical to the horizontal, the body, now moving uniformly, remaining able to ascend to the same height decelerating as the one which it had left accelerating vertically. The cause of the body’s power to continue moving, and to ascend again, was called “impetus” by Galileo, using an old term of “cause”, or “force”. But Galileo also used other terms for it, such as for example “vis impressa”, the impressed force. The underlying view was that natural entities were characterized not by their names but by their “measures”, since everything in Nature should have a specific “measure” according to an old wisdom. Consequently, natural science had to be a quantitative science, investigating the individual “measures” or quantities of the natural entities inquired, such as “motion”, “change of motion”, and “force” as its cause. Finite “spaces” and “times” of motion were measured relatively to the natural or “absolute” infinite standards of “time”, JK, and “space”, GH, as in the above diagram, that is, relatively to the absolute space-time frame of reference of motion.

On this background arouse in the second half of the 17^th century the problem of “the true measure of force”. This problem leads immediately to the centre of our discussion about what it is that in electromagnetic theory “proceeds” through a transmission line at the constant velocity c. However, in order to understand what’s going on we must add another short reflection on the “history” of science.

In the wake of René Descartes’s natural philosophy it had become a common view in the middle of the 17^th century that “force” as a cause of motion had to be measured through its effect, the generated motion; in symbols, with F for force, and p for mot-ion: F = p, or differently, as the geometers put it, F ~ p, or F/p = c = constant, with c as “proportionality constant”. But in 1686, one year before Newton’s Principia appeared in London, the German mathematician Gottfried Wilhelm Leibniz published  in the German journal “Acta eruditorum” a paper entitled “Short demonstration of a remark-able error of Descartes and others related to a natural law according to which God should always maintain one and the same quantity of motion, and how they misuse it in mechanics”. In this paper, Leibniz criticized the F = mv = p concept of “force”, developing a different law by calculating the “force” (cause of fall) of a falling body by  the distance fallen. Of course, Leibniz’s measure of “force”, later baptized “vis viva”, the living force, resulted in the “squared” relation F = mv^2, which became later on the “concept of energy”, E = mv^2/2.

Newton, however, held the view that the “force” F as cause of motion must be measured in proportion to its effect, which is motion, so that a quantity of force would generate and maintain a proportional quantity of motion: F/p = F/mv = c = constant. This is the background of Newton’s theory of force and motion, as it emerges from the Principia (def. 2 of “quantity of motion”, def. 3 of “quantity of inertial force or impetus”; def. 4 of “impressed force” to generate changes of motion, as described in Newton’s  second law of motion). The formula F/p = c relates to Newton’s concept of “force innate in matter” or “impetus” which is the force that maintains uniform straightline motion. Note that the constant c to connect force (cause) and motion (change of) as its proportional effect is the same as in Galileo’s basic law of motion described above. The different Leibnizian concept of force, or “energy”, was rejected by Newton, because Leibniz, when he derived it, had committed a “wonderfully philosophical error” (Samuel Clarke). The error was to measure the force in proportion to distance (space). Galileo had demonstrated in his “Discorsi” that in this case the falling body would occupy different places in space at the same time which is absurd and impossible. Therefore, the only realistic measure was “force proportional to time”, leading to the well-known Galilean term of acceleration [L/T^2] of free fall.

With Leibniz’s paper of 1686 there arouse a serious controversy among scientists and philosophers concerning the problem of the true measure of “force”, the so-called “vis-viva controversy”. Was the true measure of force given by mv^2, or was it given by mv? The controversy lasted over 60 years until 1746. In this year, the French philosopher Jean d’Alembert published a book in which he proposed to measure the basic “force” according to the measure of mass-acceleration, d(mv)/dt, and to gain on this basis by integrating over space (i.e. by the line integral of d(mv)/dt) the measure mv^2, and by integrating over time the measure mv. Thus the term d(mv)/dt seemed to be the common “root of” the controversial concepts, which view finally settled the vis-viva controversy.      

This Leibnizian method became the foundation of “classical mechanics”, as is well-known. In this context, however, the Leibnizian concept of “energy” advanced to be the only practically relevant “measure of force”, so that it, symbolized by H, even became the basic concept of the Hamilton-Jacobi form of mechanics, or “dynamics”, as the new science was called, following (not only) the terminology of Leibniz (cf. his “Specimen Dynamicum” of 1695). Note that Newton never used neither the terms nor the concepts of “energy” and “dynamics”. Note also, however, that nobody ever has noticed, much less corrected the “wonderfully philosophical error” which the Leibnizian energy concept is based on, even though Samuel Clarke had made the error public in a published correspondence he entertained, as Newton’s amanuensis, with Leibniz during the years 1715/1716 (the famous “Leibniz-Clarke –Correspondence”).

In the first half of the 19th century scientists (engineers) learned by experience and experiment that neither the time-reversible concept of “force”, d(mv)dt, nor the scalar concept of “energy”, mv^2/2, was able to describe the natural process of generation of motion in the direction of time as required according to natural experience (the “time-arrow”). As a consequence they developed the new science of thermodynamics” on a partly different foundation.

In the second half of the 19^th century James Clerk Maxwell developed his mathematical theory of electromagnetism, based on Michael Faraday’s mainly experimental discoveries. Maxwell, as he says it in the Preface to the First Edition of his 1873 “Treatise”, endeavoured “to place in as clear a light as I can the relations between the mathematical form of this theory and that of the fundamental science of Dynamics”. This, however, meant to uncritically apply the basic principles of Leibnizian “dynamics” unconscious of their implicit deficiencies as outlined above. The result was the electromagnetic theory the principles of which we are now discussing, inconsistent as they are due to Maxwell uncritically presupposing as granted the principles of Lei-nizian “dynamics”.

In your email of yesterday, which I received at 14.29 h local time, you write:

“Basically, I am struggling in defining what momentum p is in terms of Catt.”

As I see things, we should at first see what momentum p is in terms of Maxwell. Did he take the term p = mv for “electromagnetic momentum”?  

– And here I must stop today. What I will do next is to disentangle the confusion of concepts that characterizes Maxwell’s theory and Ivor Catt’s as well. This has first required –inevitably from my point of view – to show where the Non-Newtonian concept of scalar “energy” (uncritically used by both Maxwell and Catt) stems from, and what its deficiency is; you find the analysis and the result above.

In my next mail I wrote:

Alex:

 

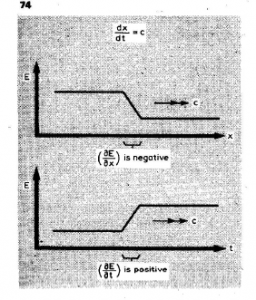
While I am waiting for your comments, here is the crucial diagram from Ivor’s paper: The Heaviside Signal

It shows the relationship: 

that is equivalent (Right?) to your definition of c as the constant geometric proportionality coefficient,

as long as we agree that dE/dx (spatial energy density) is equivalent to momentum p and dE/dt is equivalent to your E (temporal energy intensity, aka power).

What do you think about all this (together with my earlier points)?

 

To which Ed agrees:

Ed:

In addition to what I just have sent you I agree that this diagram and your explanation results exactly in E/p = c = constant,

E representing a vector quantity in linear relation to p, and therefore different from the scalar E proportional to p^2 of classical mechanics and Maxwell’s theory.

As we now can see, momentum (dE/dx in your example, identical with Catt’s paper, Appendix 1) plays a central role in this context.

And that’s what he just sent to me prior to that:

Ed:

in my first reply I outlined the history of concepts of “cause” and “effect” in the theory of motion to show the confusion about the concepts of “force” and “energy” as “cause”. But the overview also shows that the concept of “effect”, that is, the concept of “momentum” p = mv, dimensions [ML/T], has not changed since the time of Galileo and Newton. As my last proposal was to look what p means in Maxwell’s theory, I want to point to his “Treatise”, vol. I, paragraph 6 “Derived Units”. Here he introduces “momentum” as “unit of mass moving with unit of velocity”, the dimensions of p being [ML/T] accordingly. So we see Maxwell’s concept of momentum to be identical withGalileo’s and Newton’s.

But we also see here confusion arise as Maxwell next introduces “force which produces unit of momentum” with units [ML/T^2]. This alleged “force” to produce “momentum” then works by integrating the force over time, which is certainly mathematically possible, but mathematically only (applying the calculus). It has nothing to do with reality, that is, generation of an effect by a cause in space and time. Therefore Maxwell’s “force” [ML/T^2], identical with the “force” of classical Non-Newtonian mechanics, is certainly not the real generating cause of motion (momentum). Note that this “force” of dimensions [ML/T^2] “is” nothing other but “the rate of change of momentum in time”, d(mv)/dt, so it is qualitatively (“genetically”) identical with “momentum”, and cannot therefore stand for the heterogeneous “cause” to “produce” momentum.

Now, to answer your question “what momentum p is in terms of Catt” I refer to Catt’s paper “The Heaviside Signal” as well as you. Here Catt says that the Heaviside signal “always contains one kind of energy only, which is equal to the product of E and H at that point”. This product ExH, divided by c he calls “energy density” here, but somewhat later only ExH is called “density”, and next he calls ExH the “Poynting vector”, and then the “energy current”. Nowhere does the term “momentum” appear in this paper. In a mail of 6 Sept. Catt even asserted that momentum p has no place in his “universe of discourse”.

The fact  is, however, that Catt’s ExH must be understood as simply the “cause” of momentum p, since divided by the constant c it just produces p. Catt writes “ExH/c = Energy density” but is not aware that this “energy density” is just momentum p. Of course, Catt’s term ExH must represent what we (you and me) have identified as “vector energy”, because only this vector energy, not the scalar energy of classical mechanics, can, devided by c, produce p. Here we meet with the difference between scalar energy and vector energy for the first time, which Maxwell did not realize, so far as I can see, nor does Ivor Catt. Therefore, as far as momentum p is concerned, I agree: Momentum p is exactly what Catt calls “energy density”. It is also true that this momentum “propagates in transmission line together with ExH”, as you put it.

Next stage: You infer that this momentum p “may hit some finite mass with the effect of mv” so that this mass moves with velocity v”.

This I doubt. Momentum p is not “mass” and not “velocity”, and not necessarily a material something. It is a natural entity in its own right, only the measure of which is dimensionally equal to the measure “mass times velocity”. So, if some finite mass is hit with momentum p = mv, for example an elementary particle, m, which is at rest, and is fixed in a compound so that it cannot leave its place (move, that is), the hit particle will somehow oscillate, and respond to the hit according to the rules of perfect elastic collision.This means that the particle will take the momentum, react by oscillating proportionally, and will pass this vector effect to its neighbour without moving itself, and so it happens with the neighbour particle, and so on, as can be seen in the case of “Newton’s cradle”. The process of “passing” will certainly not happen “instantaneously” but in time and space, even though very, very swift, (not at velocity v!), according to observation. Provided the pendulum line is long enough, so that one can measure the time it takes to propagate the momentum through the resting pendulums over a certain distance, dividing the distance by the time will yield the “velocity of momentum transfer”, which in the ideal case should equal c. Right?

//////////////////////////////////

To this I can state that, in the Wakefield experiment quoted in my paper “Energy current and computing” https://royalsocietypublishing.org/doi/full/10.1098/rsta.2017.0449

I am putting that effectively dE/dt (power or Poynting vector) causes momentum p (in our terms now dE/dx – energy density), which can be observed via the oscilloscope connected to a point in the coax cable transmission line – it’s a measurement, and it can only be seen thanks to some effect in the matter – so I continue to be convinced that we have some form of energy conversion from energy current ExH to momentum p=mv, which is what is customarily called electric current! 

I later wrote to Fei Xia the following:

I think my recent discussion with Catt/Dellian hasn’t shaken my position regarding Fundamentals expressed in my paper on Energy Current and Computing.In fact it probably has enhanced it by providing better understanding of what momentum p is in terms of Heaviside signal. Some disagreement with Ed Dellian remains as to how we pass the momentum to the organs that measure it. I state that it can only be done via action on matter (with mass – hence I formulate it as ‘hit’ the matter with mv)

Dellian seems to see it immediately as moving into the world of oscillating pendulums – which then removes the effect of the propagating ExH.

But we are gradually getting to some form of convergence.

My position is closer to Catt than to established views about passing energy (only via Newton cradle), which doesn’t necessarily imply that we have a speed of light c.

Catt’s view is that EM energy can and can ONLY move with speed of  light in the medium – without any matter involved (so Newton’s cradle ain’t obvious!).

So, seeking truth on what momentum is continues …