Paper: Making (dark matter) waves – how wave interference can help model cold dark matter

Posted on by

Alex’s first first-author paper is now available on arXiv! An art piece Alex made related to this work also placed 2nd in the Art of Science competition hosted by the SAgE faculty at Newcastle. You can see more images and descriptions in Alex’s twitter thread on the paper (and the associated art piece).

This paper models the dark matter field as a single wavefunction, rather than traditional fluid variables or collisionless particles. We show explicitly how the complex phenomenology of multi-streaming (caused by collisionless particles flowing through each other) is encoded in the interference and oscillations of the wavefunction in a simple toy model. This wave model avoids the infinite density spikes which occur when evolving classical cold dark matter collapse.

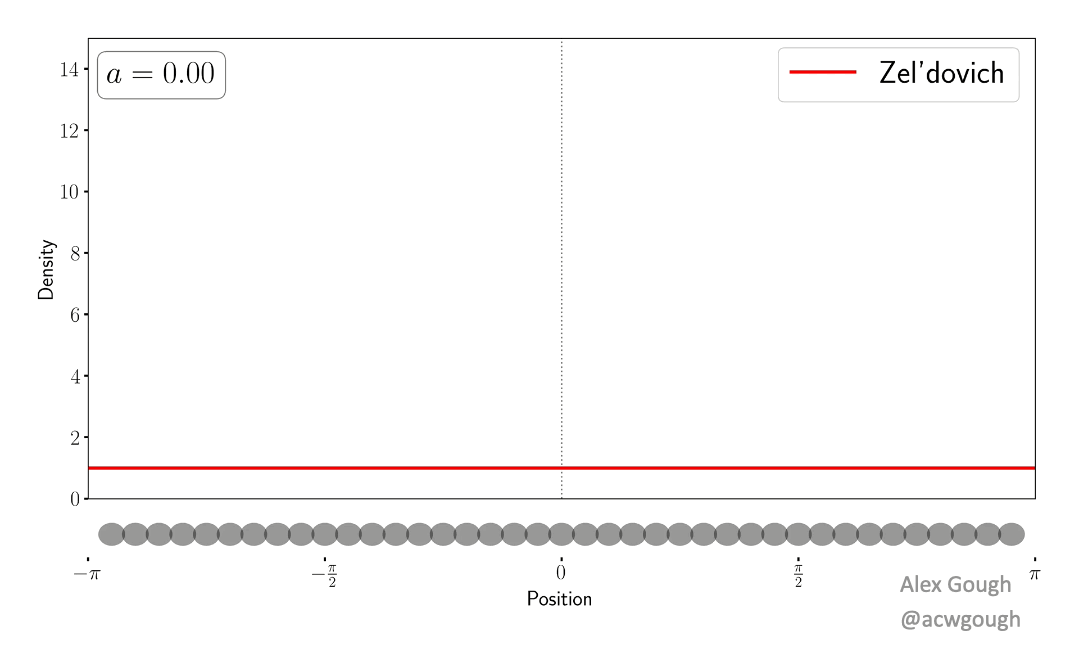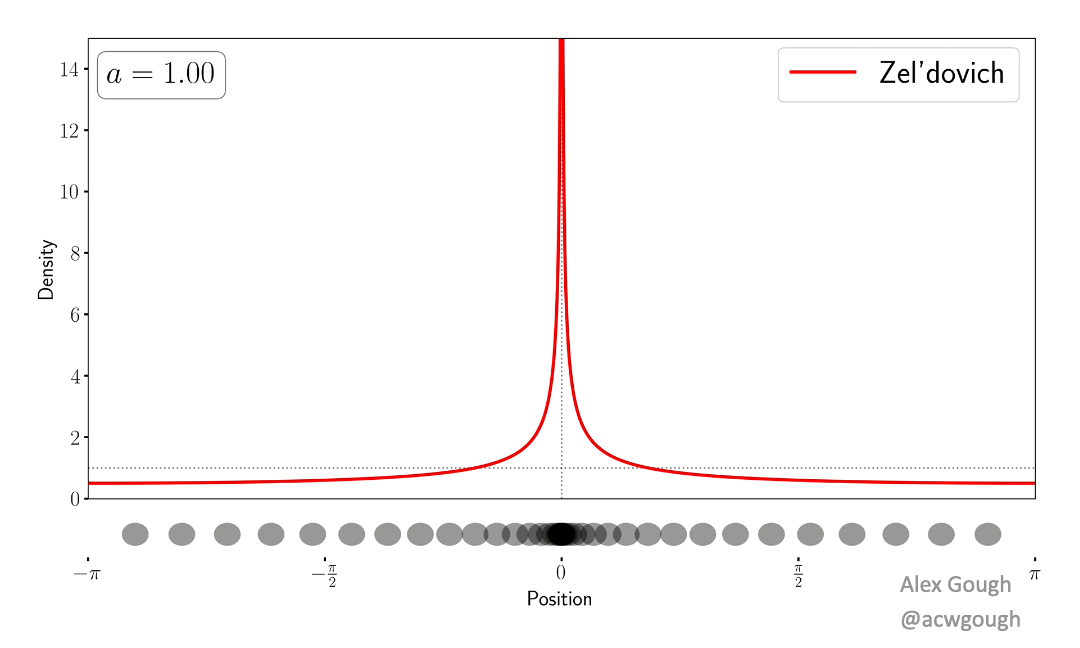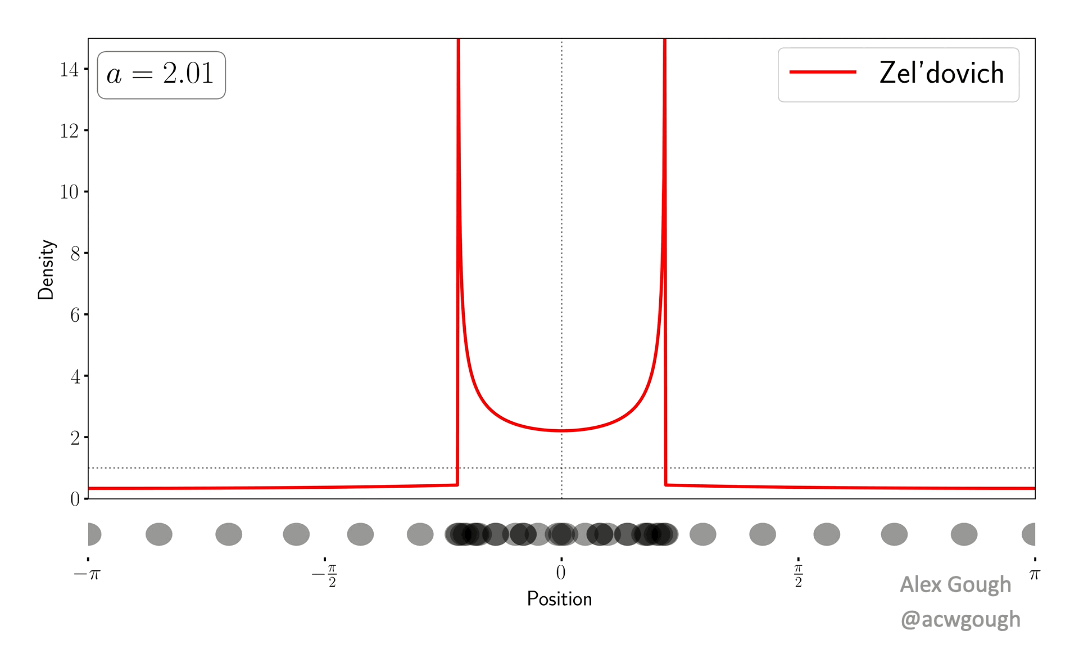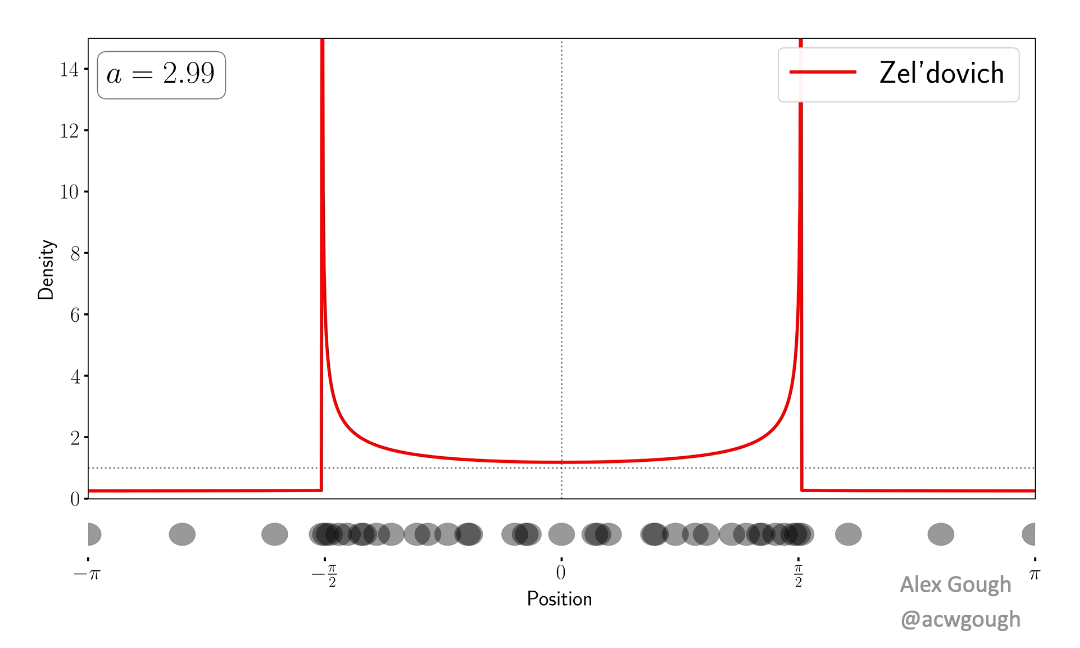
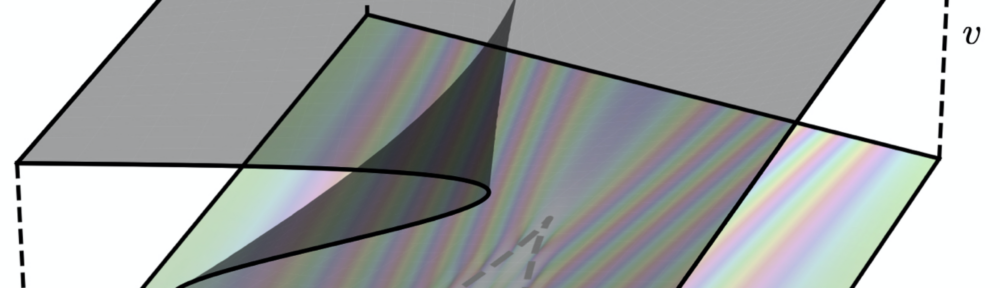
Evolution of the position and density of a set of cold dark matter particles under the Zel’dovich approximation.

This paper demonstrates how the oscillations in the wavefunction can be “unwoven” to recover a set of wavefunctions corresponding to the set of classical streams in the Zel’dovich approximation. In the multi-stream region, where the dark matter cannot be described by a perfect fluid, we demonstrate how to separate the wavefunction into an “average part”, which describes the classical fluid behaviour, and an oscillatory “hidden part” which is responsible for producing beyond perfect fluid quantities such as velocity dispersion.

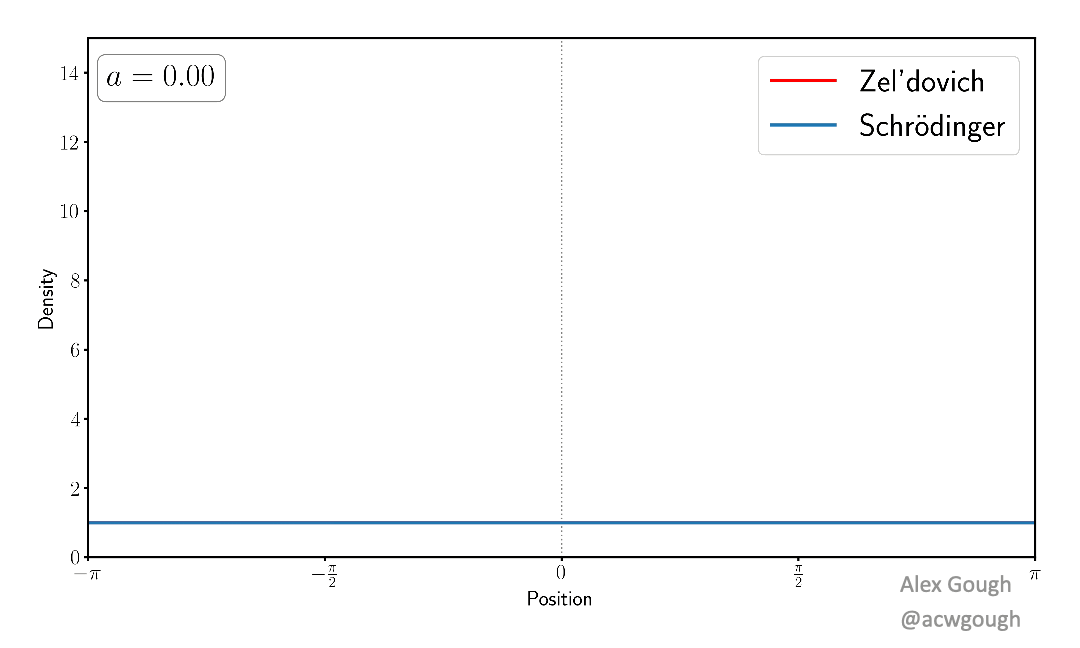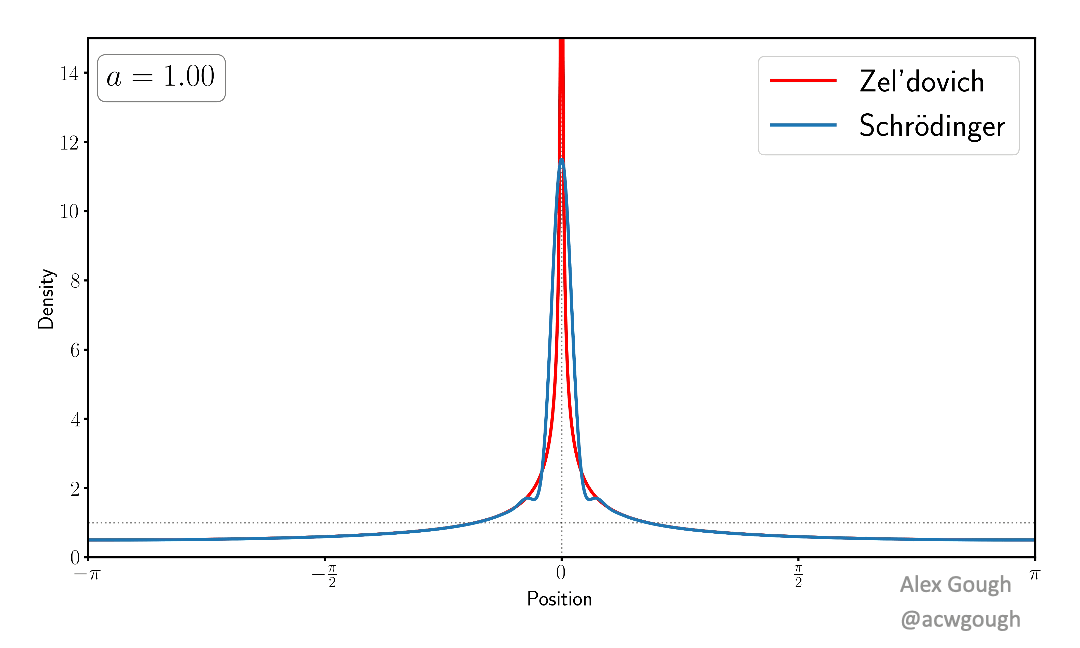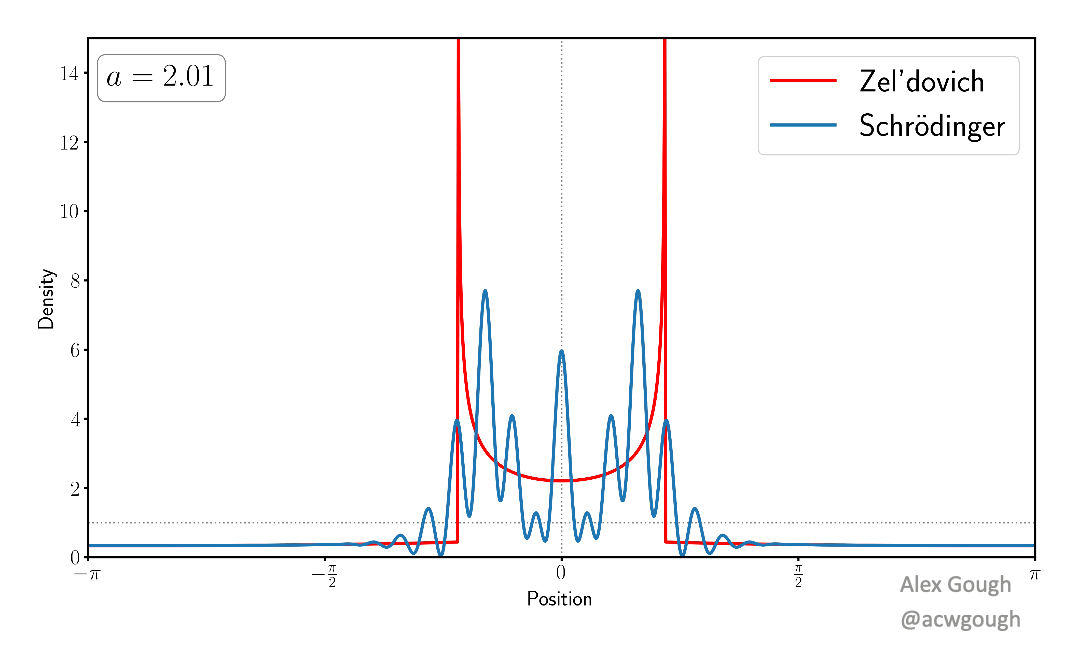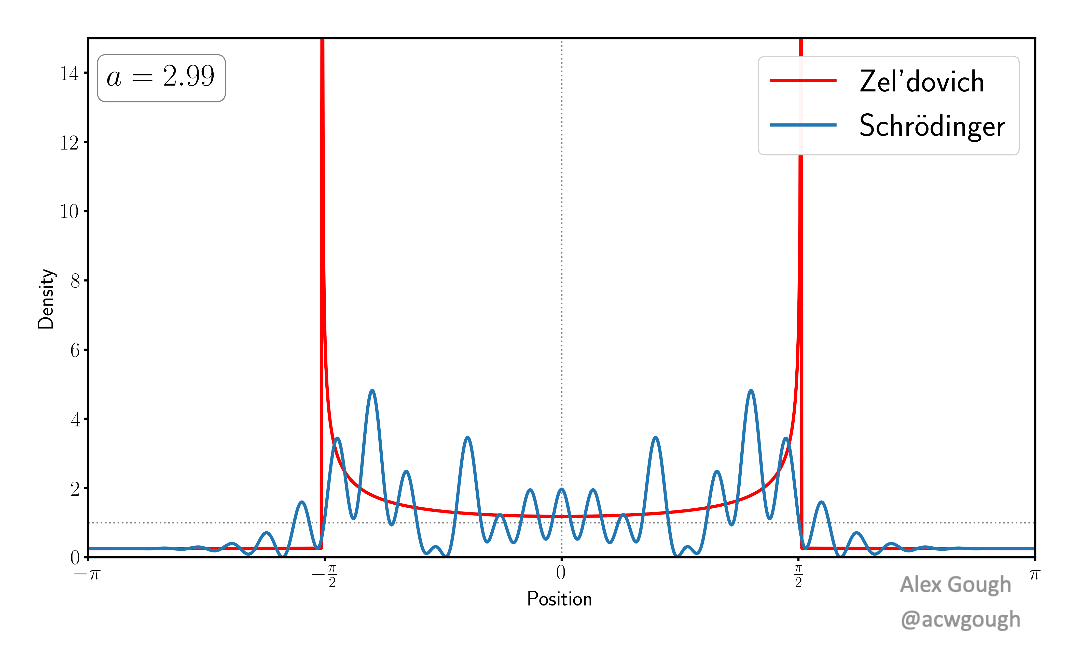
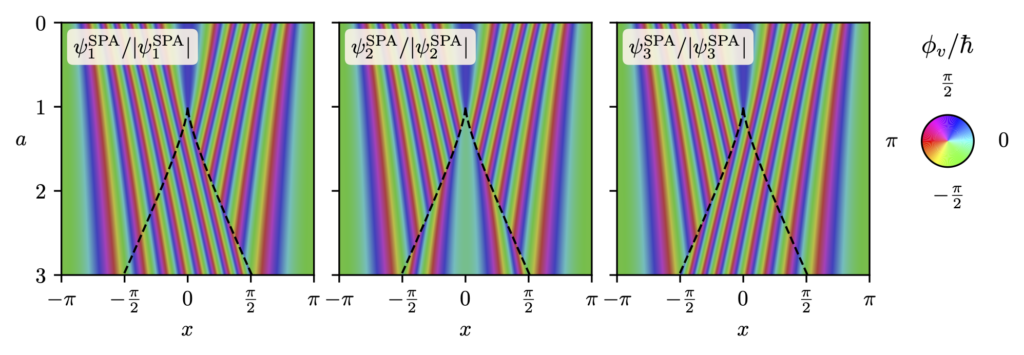
Comparison between the Zel’dovich approximation for cold dark matter and evolution of a wavefunction under the free Schrödinger equation. The wavefunction avoids the infinite density spikes (caustics) seen in classical cold dark matter, and introduces small scale interference to decorate the classical density.
Splitting of the wavefunction into three parts, each corresponding to classical dark matter trajectories.

The dense caustics formed by cold dark matter are replaced with diffraction caustics in the simple wave model, which provide classification of these caustics, and certain universal features related to the wave nature of the model. Such features are akin to those found in truly wavelike models of dark matter, such as fuzzy dark matter and ultralight axions.

The wave field corresponding to a cusp caustic. The scaling of the peak height and fringe widths are universal features, classified by catastrophe theory.