Computing connected components in an undirected graph is one of the most basic graph problems. Given a graph with n vertices and m edges, you can find its components in linear time O(n + m) using depth-first or breadth-first search. But what if you need to go faster? In this blog post, I will describe a cool new concurrent algorithm for this problem, which I learned this week at the Heidelberg Laureate Forum from Robert Tarjan himself. The algorithm distributes the work among n + m tiny processors that work concurrently most of the time and requires O(log n) global synchronisation rounds. The algorithm is remarkably simple but it’s far from obvious that it works correctly and efficiently. Happily, Tarjan and his co-author S. Cliff Liu have done all the hard proofs in their recent paper, so we can simply take the algorithm and use it.
Category Archives: algorithms
Stroll: an experimental build system
I’d like to share an experiment in developing a language-agnostic build system that does not require the user to specify dependencies between individual build tasks. By “language-agnostic” I mean the user does not need to learn a new language or a special file format for describing build tasks — existing scripts or executable files can be used as build tasks directly without modification.
I call this build system Stroll because its build algorithm reminds me of strolling through a park where you’ve never been before, trying to figure out an optimal path to your target destination, and likely going in circles occasionally until you’ve built up a complete mental map of the park.
Walking on trees
Yesterday I learned a cool algorithm, which can be intuitively described as follows:
Pick a starting node, walk as far as you can, turn around, and walk as far as you can again.
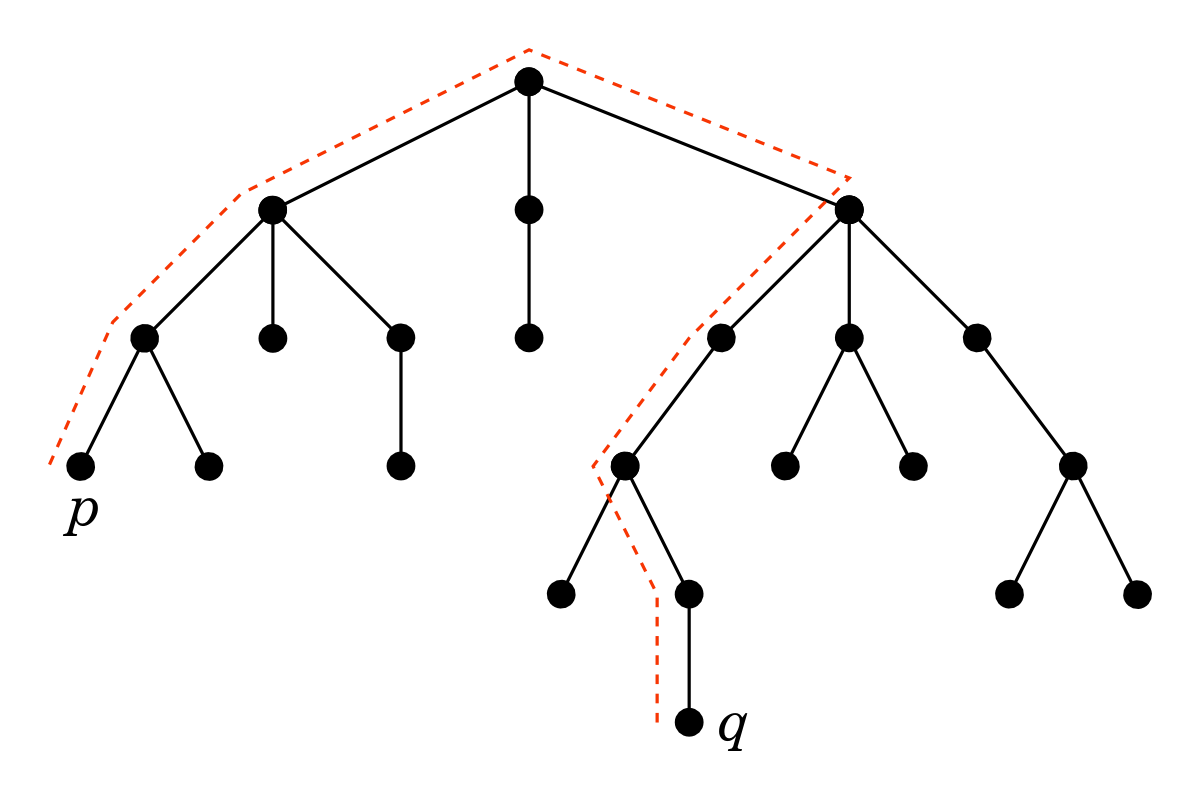
Doesn’t sound too complicated, right? But it actually solves a non-trivial problem: it finds the diameter of a tree in linear computation time. The diameter of a tree is the length of the longest possible walk on it. For example, the tree below has diameter 8, because the longest walk on it goes through 8 links. There are actually three walks of length 8, we show the one between nodes p and q:
TSP art
Want to do an optimal tour through 15112 cities in Germany or through 24978 cities in Sweden? Check out these maps: goo.gl/kp3OYj and goo.gl/ZUX1El.
These and other large instances of the the Travelling Salesman Problem (TSP) can be found at this website: http://www.math.uwaterloo.ca/tsp/index.html. In particular, check out the TSP art page. Here is my favourite, Botticelli’s Venus: