In this blog post we will explore the consequences of postulating 0 = 1 in an algebraic structure with two binary operations (S, +, 0) and (S, ⋅, 1). Such united monoids have a few interesting properties, which are not immediately obvious. For example, we will see that the axiom 0 = 1 is equivalent to a seemingly less extravagant axiom ab = ab + a, which will send us tumbling down the rabbit hole of algebraic graphs and topology.
We start with a brief introduction to monoids, rings and lattices. Feel free to jump straight to the section “What if 0 = 1?”, where the fun starts.
Monoids
A monoid (S, ∘, e) is a way to express a basic form of composition in mathematics: any two elements a and b of the set S can be composed into a new element a ∘ b of the same set S, and furthermore there is a special element e ∈ S, which is the identity element of the composition, as expressed by the following identity axioms:
a ∘ e = a
e ∘ a = a
In words, composing the identity element with another element does not change the latter. The identity element is sometimes also called unit.
As two familiar everyday examples, consider addition and multiplication over integer numbers: (ℤ, +, 0) and (ℤ, ⋅, 1). Given any two integers, these operations produce another integer, e.g. 2 + 3 = 5 and 2 ⋅ 3 = 6, never leaving the underlying set of integers ℤ; they also respect the identity axioms, i.e. both a + 0 = 0 + a = a and a ⋅ 1 = 1 ⋅ a = a hold for all integers a. Note: from now on we will often omit the multiplication operator and write simply ab instead of a ⋅ b, which is a usual convention.
Another important monoid axiom is associativity:
a ∘ (b ∘ c) = (a ∘ b) ∘ c
It tells us that the order in which we group composition operations does not matter. This makes monoids convenient to work with and allows us to omit unnecessary parentheses. Addition and multiplication are associative: a + (b + c) = (a + b) + c and a(bc) = (ab)c.
Monoids are interesting to study, because they appear everywhere in mathematics, programming and engineering. Another example comes from Boolean algebra: the logical disjunction (OR) monoid ({0,1}, ∨, 0) and the logical conjunction (AND) monoid ({0,1}, ∧, 1). Compared to numbers, in Boolean algebra the meanings of composition and identity elements are very different (e.g. number zero vs logical false), yet we can abstract from these differences, which allows us to reuse general results about monoids across various specific instances.
In this blog post we will also come across commutative and idempotent monoids. In commutative monoids, the order of composition does not matter:
a ∘ b = b ∘ a
All four examples above (+, ⋅, ∨, ∧) are commutative monoids. String concatenation (S, ++, “”) is an example of a non-commutative monoid: indeed, “a” ++ “b” = “ab” and “b” ++ “a” = “ba” are different strings.
Finally, in an idempotent monoid, composing an element with itself does not change it:
a ∘ a = a
The disjunction ∨ and conjunction ∧ monoids are idempotent, whereas the addition +, multiplication ⋅ and concatenation ++ monoids are not.
A monoid which is both commutative and idempotent is a bounded semilattice; both disjunction and conjunction are bounded semilattices.
Rings and lattices
As you might have noticed, monoids often come in pairs: addition and multiplication (+, ⋅), disjunction and conjunction (∨, ∧), set union and intersection (⋃, ⋂), parallel and sequential composition (||, ;) etc. I’m sure you can list a few more examples of such pairs. Two common ways in which such monoid pairs can be formed are called rings and lattices.
A ring, or more generally a semiring, (S, +, 0, ⋅, 1) comprises an additive monoid (S, +, 0) and a multiplicative monoid (S, ⋅, 1), such that: they both operate on the same set S, the additive monoid is commutative, and the multiplicative monoid distributes over the additive one:
a(b + c) = ab + ac
(a + b)c = ac + bc
Distributivity is very convenient and allows us to open parentheses, and (if applied in reverse) to factor out a common term of two expressions. Furthermore, ring-like algebraic structures require that 0 annihilates all elements under multiplication:
a ⋅ 0 = 0
0 ⋅ a = 0
The most basic and widely known ring is that of integer numbers with addition and multiplication: we use this pair of monoids every day, with no fuss about the underlying theory. Various lesser known tropical and star semirings are a great tool in optimisation on graphs — read this cool functional pearl by Stephen Dolan if you want to learn more.
A bounded lattice (S, ∨, 0, ∧, 1) also comprises two monoids, which are called join (S, ∨, 0) and meet (S, ∧, 1). They operate on the same set S, are required to be commutative and idempotent, and satisfy the following absorption axioms:
a ∧ (a ∨ b) = a
a ∨ (a ∧ b) = a
Like rings, lattices show up very frequently in different application areas. Most basic examples include Boolean algebra ({0,1}, ∨, 0, ∧, 1), the power set (2S, ⋃, Ø, ⋂, S), as well as integer numbers with negative and positive infinities and the operations max and min: (ℤ±∞, max, -∞, min, +∞). All of these lattices are distributive, i.e. ∧ distributes over ∨ and vice versa.
What if 0 = 1?
Now that the scene has been set and all characters introduced, let’s see what happens when the identity elements of the two monoids in a pair (S, +, 0) and (S, ⋅, 1) coincide, i.e. when 0 = 1.
In a ring (S, +, 0, ⋅, 1), this leads to devastating consequences. Not only 1 becomes equal to 0, but all other elements of the ring become equal to 0 too, as demonstrated below:
| a | = | a ⋅ 1 | (identity of ⋅) |
| = | a ⋅ 0 | (we postulate 0 = 1) | |
| = | 0 | (annihilating 0) |
The ring is annihilated into a single point 0.
In a bounded lattice (S, ∨, 0, ∧, 1), postulating 0 = 1 leads to the same catastrophe, albeit in a different manner:
| a | = | 1 ∧ a | (identity of ∧) |
| = | 1 ∧ (0 ∨ a) | (identity of ∨) | |
| = | 0 ∧ (0 ∨ a) | (we postulate 0 = 1) | |
| = | 0 | (absorption axiom) |
The lattice is absorbed into a single point 0.
Postulating the axiom 0 = 1 has so far led to nothing but disappointment. Let’s find another way of pairing monoids, which does not involve the axioms of annihilation and absorption.
United monoids
Consider two monoids (S, +, 0) and (S, ⋅, 1), which operate on the same set S, such that + is commutative and ⋅ distributes over +. We call these monoids united if 0 = 1. To avoid confusion with rings and lattices, we will use e to denote the identity element of both monoids:
a + e = ae = ea = a
We will call this the united identity axiom. We’ll also refer to e as empty, the operation + as overlay, and the operation ⋅ as connect.
What can we tell about united monoids? First of all, it is easy to prove that the monoid (S, +, e) is idempotent:
| a + a | = | ae + ae | (united identity) |
| = | a(e + e) | (distributivity) | |
| = | ae | (united identity) | |
| = | a | (united identity) |
Recall that this means that (S, +, e) is a bounded semilattice.
The next consequence of the united identity axiom is a bit more unusual:
ab = ab + a
ab = ab + b
ab = ab + a + b
We will refer to the above properties as containment laws: intuitively, when you connect a and b, the constituent parts are contained in the result ab. Let us prove containment:
| ab + a | = | ab + ae | (united identity) |
| = | a(b + e) | (distributivity) | |
| = | ab | (united identity) |
The two other laws are proved analogously (in fact, they are equivalent to each other).
Surprisingly, the containment law ab = ab + a is equivalent to the united identity law 0 = 1, i.e. the latter can be proved from the former:
| 0 | = | 1 ⋅ 0 | (1 is identity of ⋅) |
| = | 1 ⋅ 0 + 1 | (containment) | |
| = | 0 + 1 | (1 is identity of ⋅) | |
| = | 1 | (0 is identity of +) |
This means that united monoids can equivalently be defined as follows:
- (S, +) is a commutative semigroup.
- (S, ⋅, e) is a monoid that distributes over +.
- Containment axiom: ab = ab + a.
Then the fact that (S, +, e) is also a monoid can be proved as above.
Finally, let’s prove one more property of united monoids: non-empty elements of S can have no inverses. More precisely:
if a + b = e or ab = e then a = b = e.
The lack of overlay inverses follows from overlay idempotence:
| a | = | a + e | (united identity) |
| = | a + a + b | (assumption a + b = e) | |
| = | a + b | (idempotence) | |
| = | e | (assumption a + b = e) |
The lack of connect inverses follows from the containment law:
| a | = | e + a | (united identity) |
| = | ab + a | (assumption ab = e) | |
| = | ab | (containment) | |
| = | e | (assumption ab = e) |
It is time to look at some examples of united monoids.
Example 1: max and plus, united
One example appears in this paper on Haskell’s ApplicativeDo language extension. It uses a simple cost model for defining the execution time of programs composed in parallel or in sequence. The two monoids are:
- (ℤ≥0, max, 0): the execution time of programs a and b composed in parallel is defined to be the maximum of their execution times:
time(a || b) = max(time(a), time(b)) - (ℤ≥0, +, 0): the execution time of programs a and b composed in sequence is defined to be the sum of their execution times:
time(a ; b) = time(a) + time(b)
Execution times are non-negative, hence both max and + have identity 0, which is the execution time of the empty program: max(a, 0) = a + 0 = a. It is easy to check distributivity (+ distributes over max) and containment:
a + max(b, c) = max(a + b, a + c)
max(a + b, a) = a + b
Note that the resulting algebraic structure is different from the tropical max-plus semiring (ℝ−∞, max, −∞, +, 0) commonly used in scheduling, where the identity of max is −∞.
In general, various flavours of parallel and sequential composition often form united monoids. In this paper about Concurrent Kleene Algebra the authors use the term bimonoid to refer to such structures, but this term is also used to describe an unrelated concept in category theory, so let me stick to “united monoids” here, which has zero google hits.
Example 2: algebraic graphs
My favourite algebraic structure is the algebra of graphs described in this paper. The algebra comprises two monoids that have the same identity, which motivated me to study similar algebraic structures, and led to writing this blog post about the generalised notion of united monoids.
As a brief introduction, consider the following operations on graphs. The overlay operation + takes two graphs (V1, E1) and (V2, E2), and produces the graph containing the union of their vertices and edges:
(V1, E1) + (V2, E2) = (V1 ∪ V2, E1 ∪ E2)
The connect operation ⋅ is similar to overlay, but it also adds an edge from each vertex of the first graph to each vertex of the second graph:
(V1, E1) ⋅ (V2, E2) = (V1 ∪ V2, E1 ∪ E2 ∪ V1 × V2)
The operations have the same identity e — the empty graph (∅, ∅) — and form a pair of united monoids, where ⋅ distributes over +.
In addition to the laws of united monoids described above, the algebra of graphs has the axiom of decomposition:
abc = ab + ac + bc
The intuition behind this axiom is that any expression in the algebra of graphs can be broken down into vertices and pairs of vertices (edges). Note that the containment laws follow from decomposition, e.g.:
| ab | = | aeb | (e identity of ⋅) |
| = | ae + ab + eb | (decomposition) | |
| = | ae + ab + b | (e identity of ⋅) | |
| = | a(e + b) + b | (distributivity) | |
| = | ab + b | (e identity of +) |
By postulating the commutativity of the connect operation (ab = ba), we can readily obtain undirected graphs.
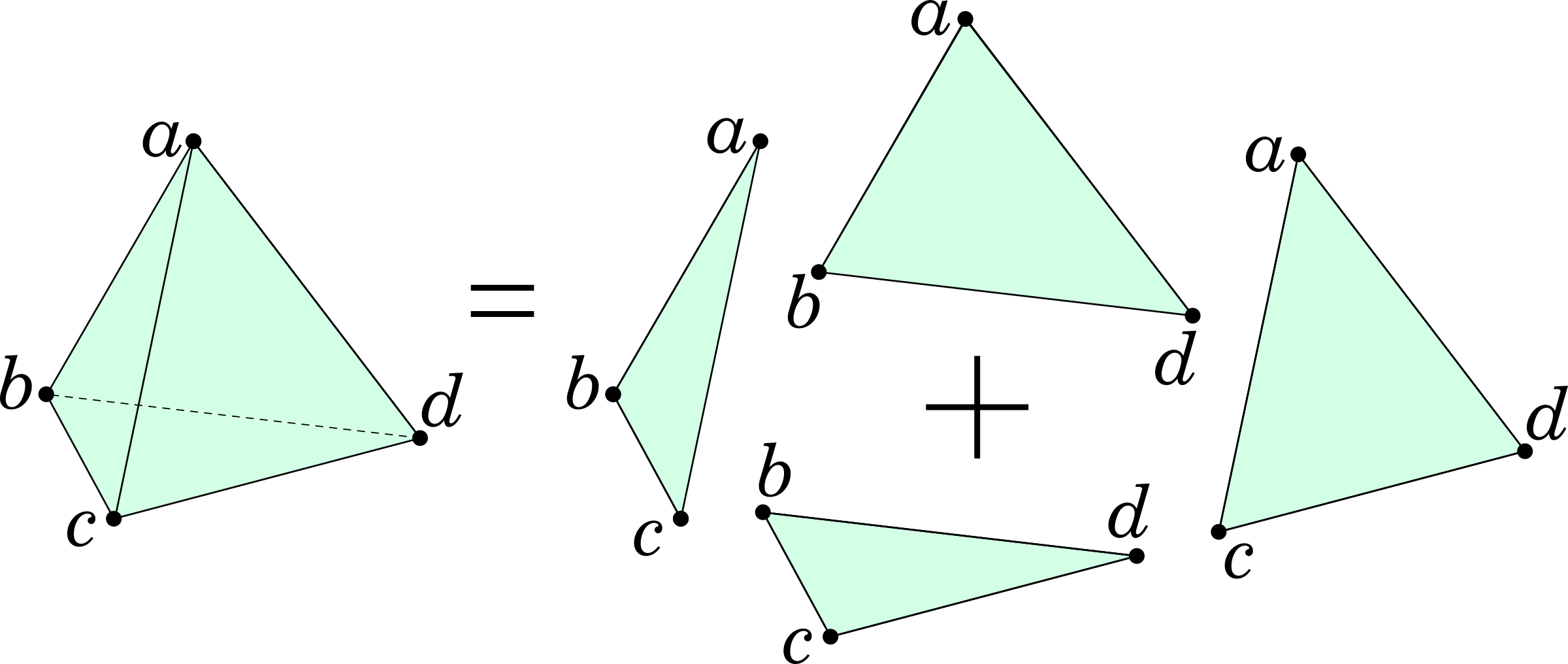
The algebra of graphs can be considered a “2D” special case of united monoids, where one can only connect elements pairwise; any 3-way connection abc falls apart into pieces. A 3-dimensional variant of the algebra can be obtained by replacing the decomposition axiom with:
abcd = abc + abd + acd + bcd
This allows us to connect vertices into pairs (edges) and triples (faces), but forces 4-way products abcd to fall apart into faces, as shown below:
Note that 3-decomposition follows from 2-decomposition: if all 3-way products fall apart then so do all 4-way products, but not vice versa. Borrowing an example from David Spivak’s paper on modelling higher- dimensional networks, such 3D graphs allow us to distinguish these two different situations:
- Three people having a conversation together, e.g. over a restaurant table. This can be modelled with a filled-in triangle abc.
- Three people having three separate tête-à-tête conversations. This can be modelled with a hollow triangle ab + ac + bc.
Similar examples show up in concurrency theory, where one might need to distinguish three truly concurrent events from three events that are concurrent pairwise, but whose overall concurrency is limited by shared resources, e.g. three people eating ice-cream with two spoons, or going through a two-person-wide door. There is a short paper on this topic by my PhD advisor Alex Yakovlev, written in 1989 (on a typewriter!).
Example 3: simplicial complexes
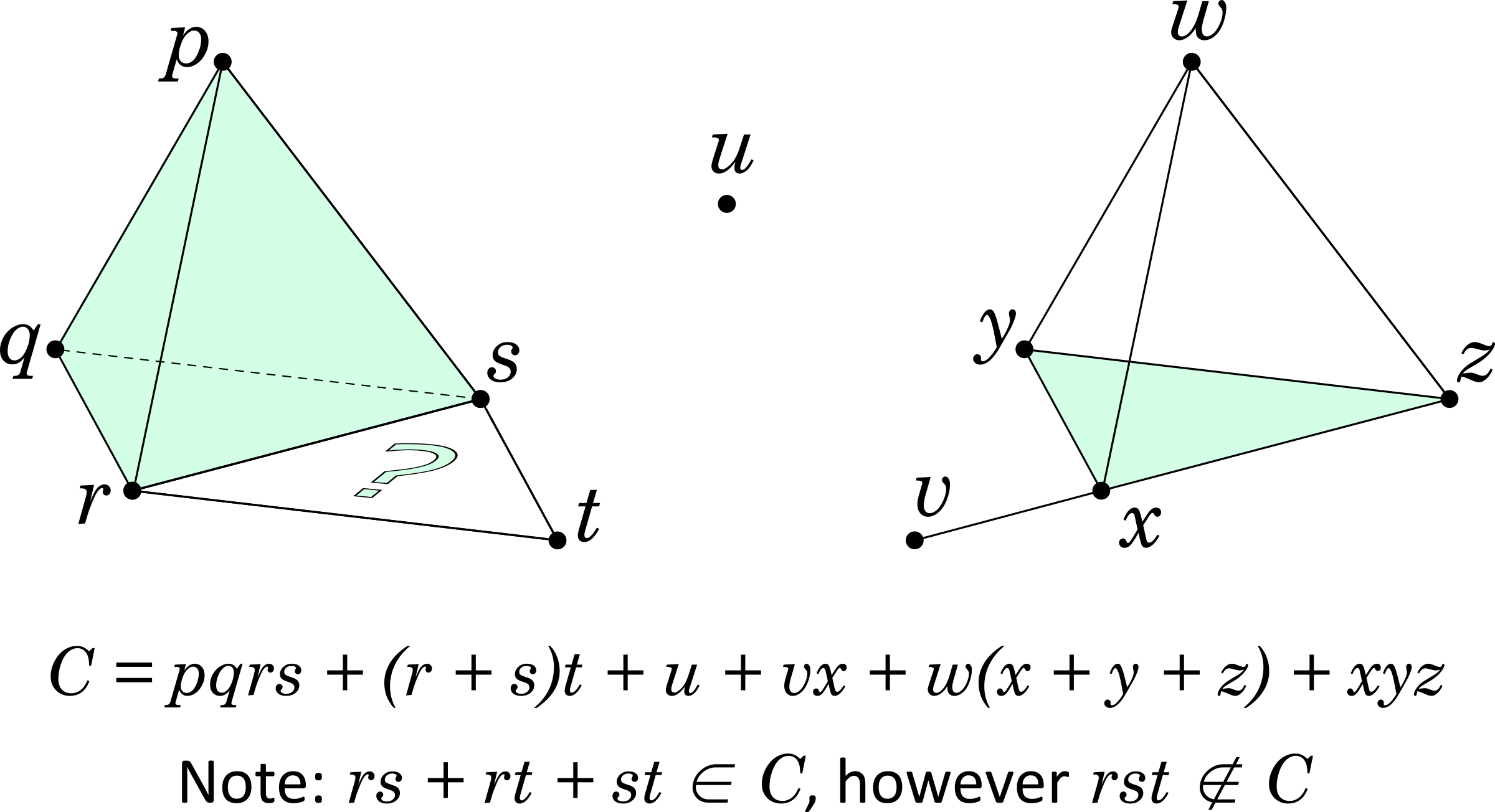
United monoids of growing dimension lead us to topology, specifically to simplicial complexes, which are composed of simple n-dimensional shapes called simplices, such as point (0-simplex), segment (1-simplex), triangle (2-simplex), tetrahedron (3-simplex), etc. — here is a cool video. We show an example of a simplicial complex below, along with a united monoid expression C that describes it, and two containment properties. We’ll further assume commutativity of connection: ab = ba.
Simplicial complexes are closed in terms of containment. For example, a filled-in triangle contains its edges and vertices, and cannot appear in a simplicial complex without any of them. This property can be expressed algebraically as follows:
abc = abc + ab + ac + bc + a + b + c
Interestingly, this 3D containment law follows from the 2D version that we defined for united monoids:
| abc | = | (ab + a + b)c | (containment) |
| = | (ab)c + ac + bc | (distributivity) | |
| = | (abc + ab + c) + (ac + a) + (bc + b) | (containment) | |
| = | abc + ab + ac + bc + a + b + c | (commutativity) |
We can similarly prove n-dimensional versions of the containment law; they all trivially follow from the basic containment axiom ab = ab + a, or, alternatively, from the united identity axiom 0 = 1.
United monoids in Haskell
Now let’s put together a small library for united monoids in Haskell and express some of the above examples in it.
Monoids are already represented in the standard Haskell library base by the type class Monoid. We need to extend it to the type class Semilattice, which does not define any new methods, but comes with two new laws. We also provide a few convenient aliases, following the API of the algebraic-graphs library:
-- Laws: -- * Commutativity: a <> b = b <> a -- * Idempotence: a <> a = a class Monoid m => Semilattice m empty :: Semilattice m => m empty = mempty overlay :: Semilattice m => m -> m -> m overlay = mappend overlays :: Semilattice m => [m] -> m overlays = foldr overlay empty infixr 6 <+> (<+>) :: Semilattice m => m -> m -> m (<+>) = overlay -- The natural partial order on the semilattice isContainedIn :: (Eq m, Semilattice m) => m -> m -> Bool isContainedIn x y = x <+> y == y
We are now ready to define the type class for united monoids that defines a new method connect and associated laws:
-- Laws: -- * United identity: a <.> empty == empty <.> a == a -- * Associativity: a <.> (b <.> c) == (a <.> b) <.> c -- * Distributivity: a <.> (b <+> c) == a <.> b <+> a <.> c -- (a <+> b) <.> c == a <.> c <+> b <.> c class Semilattice m => United m where connect :: m -> m -> m infixr 7 <.> (<.>) :: United m => m -> m -> m (<.>) = connect connects :: United m => [m] -> m connects = foldr connect empty
Algebraic graphs are a trivial instance:
import Algebra.Graph (Graph) import qualified Algebra.Graph as Graph -- TODO: move orphan instances to algebraic-graphs library instance Semigroup (Graph a) where (<>) = Graph.overlay instance Monoid (Graph a) where mempty = Graph.empty instance Semilattice (Graph a) instance United (Graph a) where connect = Graph.connect
We can now express the above simplicial complex example in Haskell and test whether it contains the filled-in and the hollow triangles:
-- We are using OverloadedStrings for creating vertices example :: (United m, IsString m) => m example = overlays [ "p" <.> "q" <.> "r" <.> "s" , ("r" <+> "s") <.> "t" , "u" , "v" <.> "x" , "w" <.> ("x" <+> "y" <+> "z") , "x" <.> "y" <.> "z" ] -- Filled-in triangle rstFace :: (United m, IsString m) => m rstFace = "r" <.> "s" <.> "t" -- Hollow triangle rstSkeleton :: (United m, IsString m) => m rstSkeleton = "r" <.> "s" <+> "r" <.> "t" <+> "s" <.> "t"
To perform the test, we need to instantiate the polymorphic united monoid expression to the concrete data type like Graph Point:
newtype Point = Point { getPoint :: String } deriving (Eq, Ord, IsString) λ> rstFace `isContainedIn` (example :: Graph Point) True λ> rstSkeleton `isContainedIn` (example :: Graph Point) True
As you can see, if we interpret the example simplicial complex using the algebraic graphs instance, we cannot distinguish the filled-in and hollow triangles, because the filled-in triangle falls apart into edges due to the 2-decomposition law abc = ab + ac + bc.
Let’s define a data type for representing simplicial complexes. We start with simplices, which can be modelled by sets.
-- A simplex is formed on a set of points newtype Simplex a = Simplex { getSimplex :: Set a } deriving (Eq, Semigroup) -- Size-lexicographic order: https://en.wikipedia.org/wiki/Shortlex_order instance Ord a => Ord (Simplex a) where compare (Simplex x) (Simplex y) = compare (Set.size x) (Set.size y) <> compare x y instance Show a => Show (Simplex a) where show = intercalate "." . map show . Set.toList . getSimplex instance IsString a => IsString (Simplex a) where fromString = Simplex . Set.singleton . fromString isFaceOf :: Ord a => Simplex a -> Simplex a -> Bool isFaceOf (Simplex x) (Simplex y) = Set.isSubsetOf x y
Note that the Ord instance is defined using the size-lexicographic order so that a simplex x can be a face of a simplex y only when x <= y.
Now we can define simplicial complexes, which are sets of simplices that are closed with respect to the subset relation.
-- A simplicial complex is a set of simplices -- We only store maximal simplices for efficiency newtype Complex a = Complex { getComplex :: Set (Simplex a) } deriving (Eq, Ord) instance Show a => Show (Complex a) where show = intercalate " + " . map show . Set.toList . getComplex instance IsString a => IsString (Complex a) where fromString = Complex . Set.singleton . fromString -- Do not add a simplex if it is contained in existing ones addSimplex :: Ord a => Simplex a -> Complex a -> Complex a addSimplex x (Complex y) | any (isFaceOf x) y = Complex y | otherwise = Complex (Set.insert x y) -- Drop all non-minimal simplices normalise :: Ord a => Complex a -> Complex a normalise = foldr addSimplex empty . sort . Set.toList . getComplex instance Ord a => Semigroup (Complex a) where Complex x <> Complex y = normalise (Complex $ x <> y) instance Ord a => Monoid (Complex a) where mempty = Complex Set.empty instance Ord a => Semilattice (Complex a) instance Ord a => United (Complex a) where connect (Complex x) (Complex y) = normalise . Complex $ Set.fromList [ a <> b | a <- Set.toList x, b <- Set.toList y ]
Now let’s check that simplicial complexes allow us to distinguish the filled-in triangle from the hollow one:
λ> example :: Complex Point u + r.t + s.t + v.x + w.x + w.y + w.z + x.y.z + p.q.r.s λ> rstFace :: Complex Point r.s.t λ> rstSkeleton :: Complex Point r.s + r.t + s.t λ> rstFace `isContainedIn` (example :: Complex Point) False λ> rstSkeleton `isContainedIn` (example :: Complex Point) True
Success! As you can check in the diagram above, the example simplicial complex contains a hollow triangle rs + rt + st, but does not contain the filled-in triangle rst.
If you would like to experiment with the code above, check out this repository: https://github.com/snowleopard/united.
Final remarks
I’ve got a few more thoughts, but it’s time to wrap up this blog post. I’m impressed that you’ve made it this far =)
Let me simply list a few things I’d like to explore in future:
-
- What about monoids that lurk in applicative functors and monads? As we know (e.g. from the final lecture of a great lecture series by Bartosz Milewski), pure :: a → m a and join :: m (m a) → m a are the monoid identity and composition in disguise. Couldn’t we unite this monoid with the monoid that corresponds to the commutative monad? Note that they have the same identity pure :: a → m a! This thought popped into my head when watching Edward Kmett’s live-coding session on commutative applicative functors and monads.
- There are cases where a single overlay monoid is united with many, possibly infinitely many connect monoids. An example comes from algebraic graphs with edge labels that have a connect operation for each possible edge label — see my Haskell eXchange 2018 talk.
- We can also define united semigroups that satisfy the containment axiom ab = ab + a but have no identity element, for example, non-empty algebraic graphs. The term “united semigroups” sounds somewhat nonsensical since semigroups have no “units”, however note that if they secretly had identity elements, they would have been the same.
- Speaking of “units”, in ring theory, a unit is any element a that has a multiplicative inverse b such that ab = 1. The lack of inverses, which we proved above, means there is only one unit in united monoids — the shared identity e.
- I have a feeling that united monoids are somehow inherently linked to Brent Yorgey’s monoidal sparks.
- We can also consider united partial monoids where the two operations may be defined only partially. For example, this paper by Jeremy Gibbons defines operations above and beside for composing directed acyclic graphs so that they both have the same identity (the empty graph), but the operation beside is defined only for graphs of matching types.
Finally, I’d like to ask a question: have you come across united monoids, perhaps under a different name? As we’ve seen, having 0 = 1 does make sense in some cases, but I couldn’t find much literature on this topic.
Update: boundary operator and derivatives
Consider the following definition of the boundary operator:
∂x = overlay { a | a < x }
where the overlay is over all elements of the set, and a < b denotes strict containment, i.e.
a < b ⇔ a + b = b ∧ a ≠ b
First, let’s apply this definition to a few basic simplices:
∂a = empty
∂(ab) = a + b + empty = a + b
∂(abc) = ab + ac + bc + a + b + c + empty = ab + ac + bc
This looks very similar to the boundary operator from topology, e.g. the boundary of the filled-in triangle abc is the hollow triangle ab + ac + bc, and if we apply the boundary operator twice, the result is unchanged, i.e. ∂(ab + ac + bc) = ab + ac + bc.
Surprisingly, the boundary operator seems to satisfy the product rule for derivatives for non-empty a and b:
∂(ab) = ∂(a)b + a∂(b)
I’m not sure where this is going, but it’s cool. Perhaps, there is a link with derivatives of types?
Thanks to Dave Clarke who suggested to look at the boundary operator.
Further update: One problem with the above definition is that the sum rule for derivatives doesn’t hold, i.e. ∂(a + b) ≠ ∂(a) + ∂(b). Sjoerd Visscher suggested to define ∂ using the desired (usual) laws for derivatives:
∂(ab) = ∂(a)b + a∂(b)
∂(a + b) = ∂(a) + ∂(b)
Coupled with ∂(empty) = ∂(a) = empty (where a is a vertex), this leads to a different boundary operator, where the boundary of the filled-in triangle abc is the hollow triangle ab + ac + bc, and the boundary of the hollow triangle is simply the three underlying vertices a + b + c:
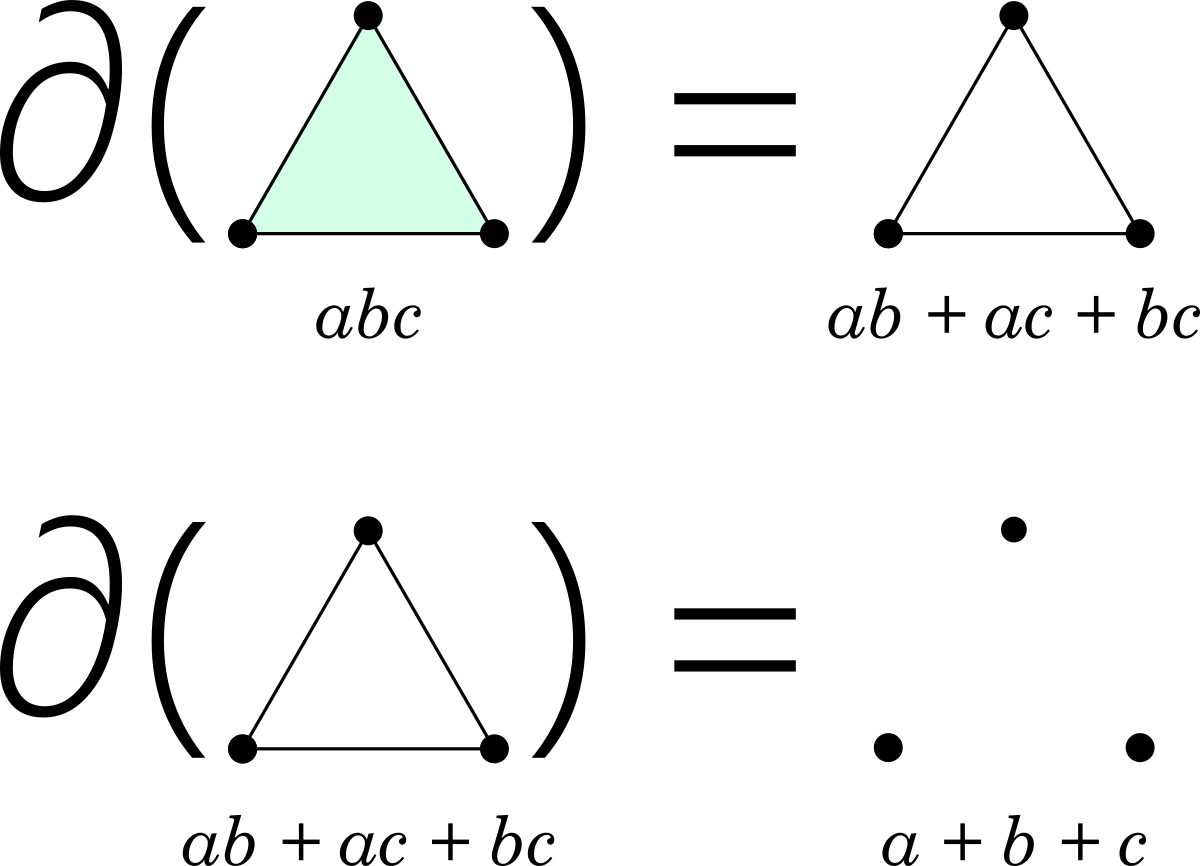
This definition of the boundary operator reduces the “dimension” of a united monoid expression by 1 (unless it is already empty).
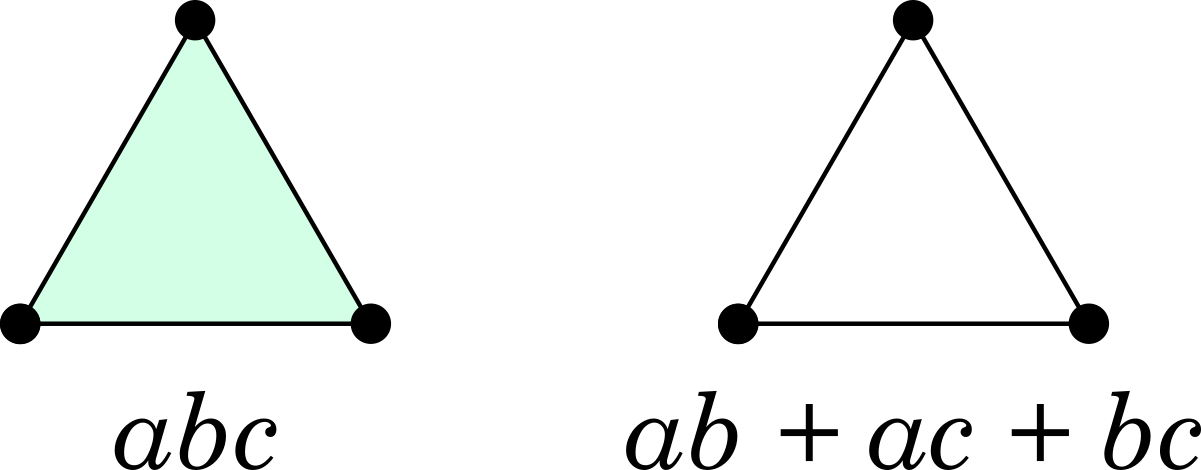
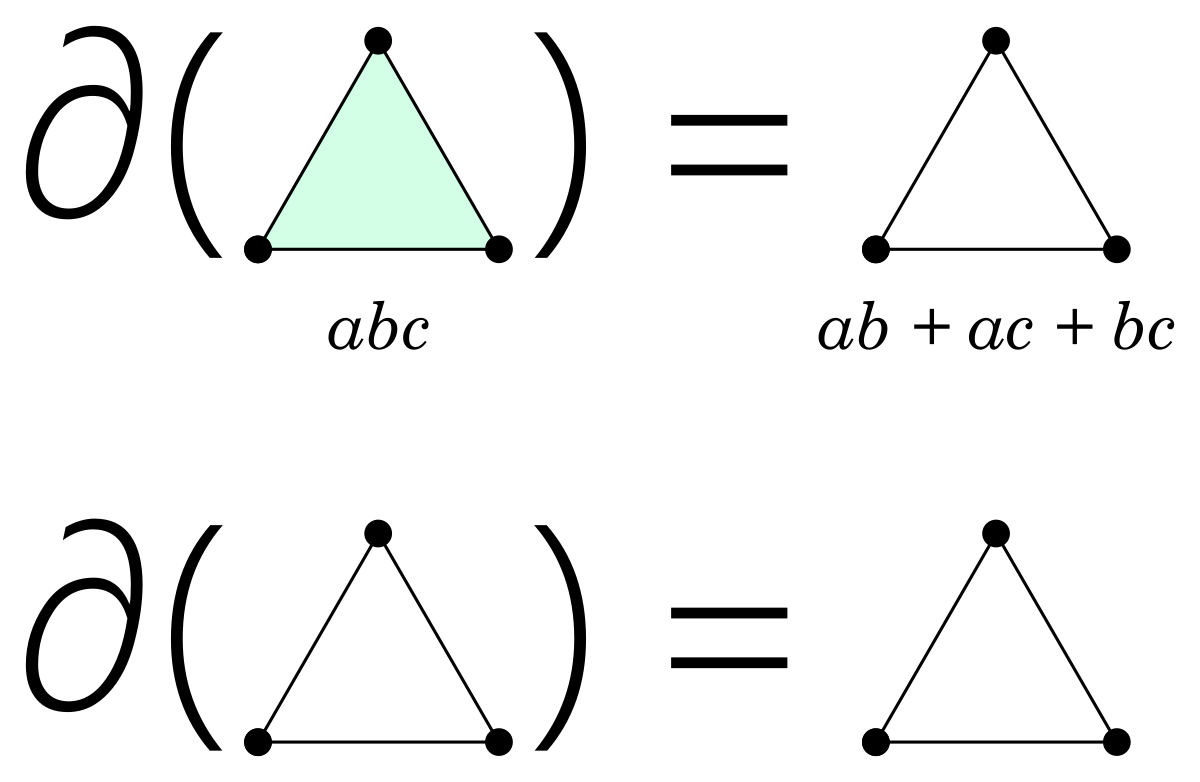
I too was inspired by algebraic graphs, and at the time I first heard of them, I was already looking at something that seemed similar (and also similar to one of your future areas of exploration) – “sequential” and “parallel” `Applicative` instances. E.g., Either/Validation and IO/Concurrently in Haskell.
I’m curious whether these relationships form “united monoids in the category of endofunctors”, with `(S, +, ⋅, e)` as something like `Semigroup a => (Either a, liftA2, liftA2 . eitherToValidation, pure)` and similarly with `(IO, liftA2, liftA2 . Concurrently, pure)`.
That is, with the sequential instance being the additive operation and the parallel instance being the multiplicative. I haven’t tried to formalize this, have at least implemented things that look reasonable. I’m very interested in what you think about it.
Hi Greg, good to hear from you!
Your earlier comments about potential links between the algebra of graphs and applicative functors and monads were one of the motivating factors behind this blog post, so thank you =)
> That is, with the sequential instance being
> the additive operation and the parallel
> instance being the multiplicative.
I guess it should be vice versa: parallel ~ additive, sequential ~ multiplicative, because we require that the additive (overlay) structure forms a commutative monoid.
I haven’t managed to implement anything yet, I’m still at the stage of exploring and writing down some rather abstract ideas, like in this blog post. Please let me know if you come up with anything that is more concrete!
Yes, sorry, I swapped parallel/sequential there (and I just came back to this page and saw your response). I was also wondering if there is a weaker form where neither monoid is commutative. E.g., `Either (MultiSet a) b` forms a united monoid, but the more common (and also sometimes more useful) `Either (NonEmpty a) b` doesn’t. But I’m hoping there’s _some_ notion that still relates the two `Applicative` instances.
Yes, I was wondering about the commutativity requirement for the underlying monoid too. It’s almost forced, i.e. any element commutes with its contents: ab + a = ab = a + ab, but of course this doesn’t hold in general unless we enforce commutativity.
Could you clarify in which sense `Either (MultiSet a) b` is a united monoid, and `Either (NonEmpty a) b` isn’t?
By the way, I have some progress in proving that Applicative and Monad are united monoids, and even algebraic graphs! Here is some work-in-progress code:
https://github.com/snowleopard/united/blob/master/src/Data/Functor/United.hs
I plan to write a follow-up blog post about this soon.
The notion of (normal) duoidal categories in https://ncatlab.org/nlab/show/duoidal+category sounds the same as united monoids to me.
If that’s true, then Applicative and Monad form a united monoid like (Type → Type, Day, Compose, Identity), right?
It seems to me that duoidal categories comprise a monoid and a comonoid, i.e. not two monoids. Or am I mistaken?
> Applicative and Monad form a united monoid like
> (Type → Type, Day, Compose, Identity), right?
I think so, yes! But I don’t yet see how this is related to duoidal categories.
I _think_ duoidal categories are two monoids, It does mention that
> J is a ⋄-monoid and I is a ⋆-comonoid
but J and I are the identities of the two monoids, and when it’s “normal”, J == I, and in the case of Applicative/Monad, J == I == Identity, and Identity is both a monoid and comonoid in the category of endofunctors.
And in https://ncatlab.org/nlab/show/duoidal+category#examples, it talks about “The category C=[V,V]C=[V,V] of endofunctors” and names *Set* and composition & Day convolution.
Thanks Greg!
I’m lacking a lot of CT vocabulary to understand the linked page fully, but I think it starts to make some intuitive sense to me 🙂
I tried to leave a comment here before but it disappeared into the aether. So I shall try again. If there are two, awaiting moderation or something, ignore one.
All I wished to say was that ‘xor’ for the addition, ‘or’ for the multiplication, and ‘false’ for the unit make a simple example.
Thanks for your comment, and I’m sorry it got lost before.
In united monoids, multiplication needs to distribute over addition, but I don’t think this holds in your example:
1 = 1 or (0 xor 0) != (1 or 0) xor (1 or 0) = 0
It also doesn’t work the other way around:
0 = 1 xor (0 or 1) != (1 xor 0) or (1 xor 1) = 1
The only pair where `xor` is distributive is `and` and `xor`:
a and (b xor c) = (a and b) xor (a and c)
which forms the basis of the GF(2) field. But I don’t see how to turn this into a united monoid since `and` and `xor` have different units.
> A monoid which is both commutative and idempotent is a bounded semilattice; both disjunction and conjunction are bounded semilattices.
Actually, semilattices are commutative and idempotent semigroups. If you require that there be a neutral element, it becomes a bound, but from the wrong (usually treated as lower) side (if looking at semilattices as posets – a ≤ b ⇔ ab = b). A semilattice needn’t in general have a bound with respect to the binary operation (i.e. its zero element), an example can be obtained by taking finite subsets of an infinite set with set sum as the operation. (Incidentally, it’s a monoid, it has a lower bound: the empty set. If you don’t like it, just drop it, the rest is a substructure as a semigroup, also a commutative and idempotent, and a semilattice without any bounds as a poset.)
(Apologies for replying so late! For some reason I didn’t receive a notification about your comment.)
I agree that semilattices needn’t, in general, have a bound, and I believe that I didn’t claim otherwise.
The quoted text says “a monoid which is both commutative and idempotent is a bounded semilattice”, which is a correct statement, isn’t it?
Would Union and disjoint Union form such a United monoid pair? e=\emptyset. Union is idempotent. Disjoint Union as multiset.
Interesting! It seems to me that this is Example 1 (max and plus, united) from the blog post, but somewhat disguised.
Union takes the maximum of element multiplicities in multisets, and disjoint union adds them up.
Do you agree?