In this blog post we will look at an example of using the algebra of graphs for manipulating sequences of items, which at first sight might not look like graphs, but are actually dependency graphs in disguise. We will develop a tiny DSL for composing todo lists on top of the alga library and will show how it can be used for planning a holiday and, on a more serious note, for writing software build systems. This blog post will partially answer the question about possible applications of the algebra of graphs that was asked in this reddit discussion.
Update: This series of blog posts was published as a functional pearl at the Haskell Symposium 2017.
Todo lists and the algebra of graphs
Todo lists are sequences of items that, as one would expect, need to be done. The order of items in the sequence matters, because some items may depend on others. The simplest todo list is the empty one. Then we have todo lists containing a single item, from which we can build up longer lists using the same operators we introduced to construct graphs.
An item will correspond to a graph vertex. We’ll use the OverloadedStrings GHC extension, so we can create todo items without explicitly wrapping them into a vertex. This will also allow everyone to choose their favourite representation for strings; plain old String is fine for our examples:
{-# LANGUAGE OverloadedStrings #-}
import Data.String
import Algebra.Graph
import Algebra.Graph.Util
instance (IsString a, Ord a) => IsString (Todo a) where
fromString = vertex . fromString
shopping :: Todo String
shopping = "presents"
Here Todo is a Graph instance whose implementation will be revealed later. One can combine several items into a single todo list using the overlay operator + of the algebra:
shopping :: Todo String shopping = "presents" + "coat" + "scarf"
The semantics of a todo list is just a list of items in the order they can be completed, or Nothing if the there is no possible completion order that satisfies all dependency constraints between different items. We can extract the semantics using todo function with the following signature:
todo :: Ord a => Todo a -> Maybe [a]
The overlay operator is commutative, therefore reordering items in the shopping list does not change the semantics:
λ> todo shopping Just ["coat","presents","scarf"] λ> todo $ "coat" + "scarf" + "presents" Just ["coat","presents","scarf"] λ> shopping == "coat" + "scarf" + "presents" True
As you can see, the items are simply ordered alphabetically as there are no dependencies between them. Let’s add some! To do that we’ll use the connect operator → from the algebra. When two todo lists are combined with →, the meaning is that all items in the first list must be completed before we can start completing items from the second todo list. I’m currently planning a holiday trip to visit friends and therefore will need to pack all stuff that I buy before travelling:
holiday :: Todo String holiday = shopping * "pack" * "travel" λ> todo holiday Just ["coat","presents","scarf","pack","travel"] λ> shopping == holiday False λ> shopping `isSubgraphOf` holiday True
Items "pack" and "travel" have been appended to the end of the list even though "pack" comes before "presents" alphabetically, and rightly so: we can’t pack presents before we buy them!
Now let’s add a new dependency constraint to an existing todo list. For example, I might want to buy a new scarf before a coat, because I would like to make sure the coat looks good with the new scarf:
λ> todo $ holiday + "scarf" * "coat" Just ["presents","scarf","coat","pack","travel"]
Look how the resulting list changed: "coat" has been moved after "scarf" to meet the new constraint! Of course, it’s not too difficult to add contradictory constraints, making the todo list impossible to schedule:
λ> todo $ holiday + "travel" * "presents" Nothing
There is nothing we can do to complete all items if there is a circular dependency in our todo list: "presents" → "pack" → "travel" → "presents".
It may sometimes be useful to have some notion of item priorities to schedule some items as soon or as late as possible. Let me illustrate this with an example, by modifying our todo lists as follows:
shopping :: Todo String shopping = "presents" + "coat" + "phone wife" * "scarf" holiday :: Todo String holiday = shopping * "pack" * "travel" + "scarf" * "coat"
As you see, I now would like to phone my wife before buying the scarf to make sure it also matches the colour of one of her scarves (she has a dozen of them and I can’t possibly remember all the colours). Let’s see how this changes the resulting order:
λ> todo holiday Just ["phone wife","presents","scarf","coat","pack","travel"]
This works but is a little unsatisfactory: ideally I’d like to phone my wife right before buying the scarf. To achieve that I can amend the shopping list by changing the priority of the item "phone wife":
-- Lower the priority of items in a given todo list low :: Todo a -> Todo a shopping :: Todo String shopping = "presents" + "coat" + low "phone wife" * "scarf" λ> todo holiday Just ["presents","phone wife","scarf","coat","pack","travel"]
Aha, this is better: "phone wife" got scheduled as late as possible, and is now right next to "scarf", as desired. But wait — if my wife finds out that I gave a low priority to my phone calls to her, I’ll get into trouble! I need to find a better way to achieve the same effect. In essence, we would like to have a variant of the connect operator that pulls the arguments together as close as possible during scheduling (and, alternatively, we may also want to repel arguments as far from each other as possible).
-- Pull the arguments together as close as possible (~*~) :: Ord a => Todo a -> Todo a -> Todo a -- Repel the arguments as far as possible (>*<) :: Ord a => Todo a -> Todo a -> Todo a shopping :: Todo String shopping = "presents" + "coat" + "phone wife" ~*~ "scarf"
This looks better and leads to the same result as the code above.
The final holiday expression can be visualised as follows:
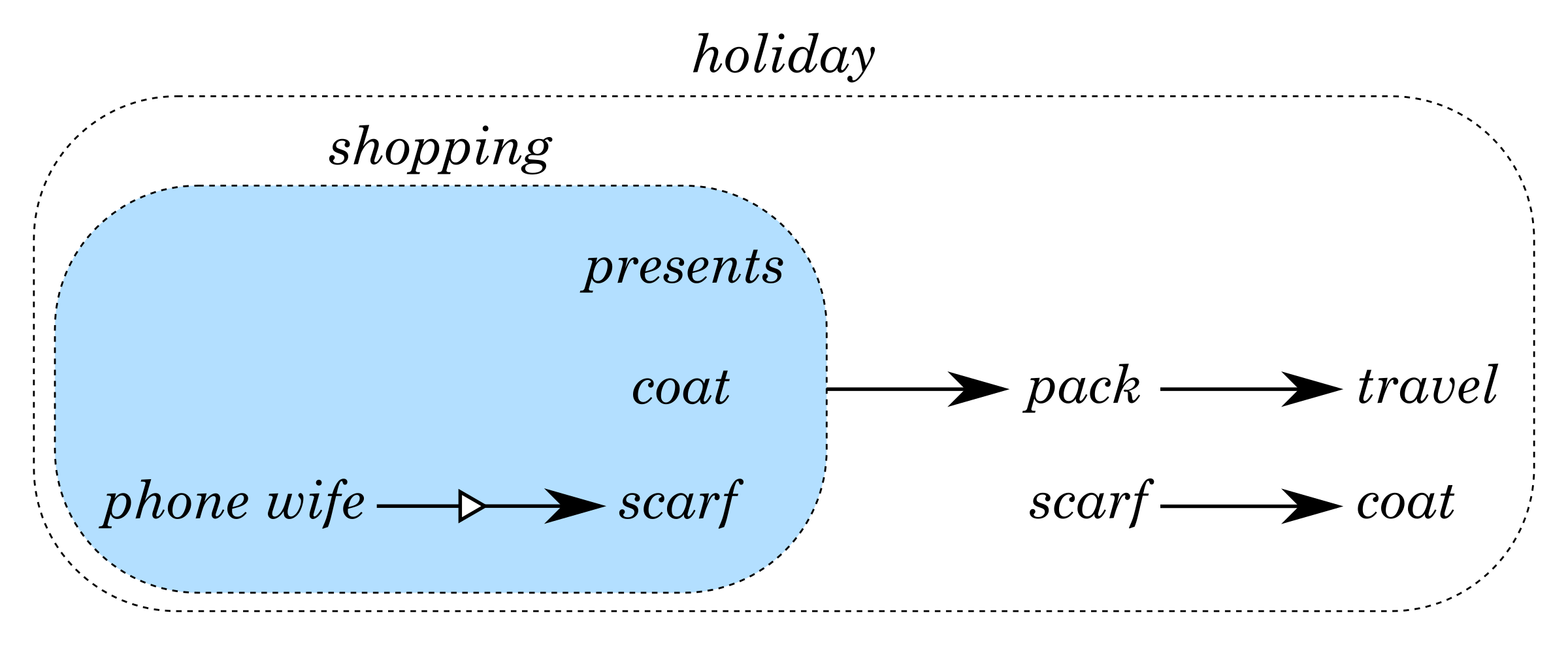
Here the overlay operator + is shown simply by placing its arguments next to each other, the connect operators are shown by arrows, and the arrow with a small triangle stands for the tightly connect operator ~*~. By following the laws of the algebra, we can flatten the graph expression into a dependency graph shown below:
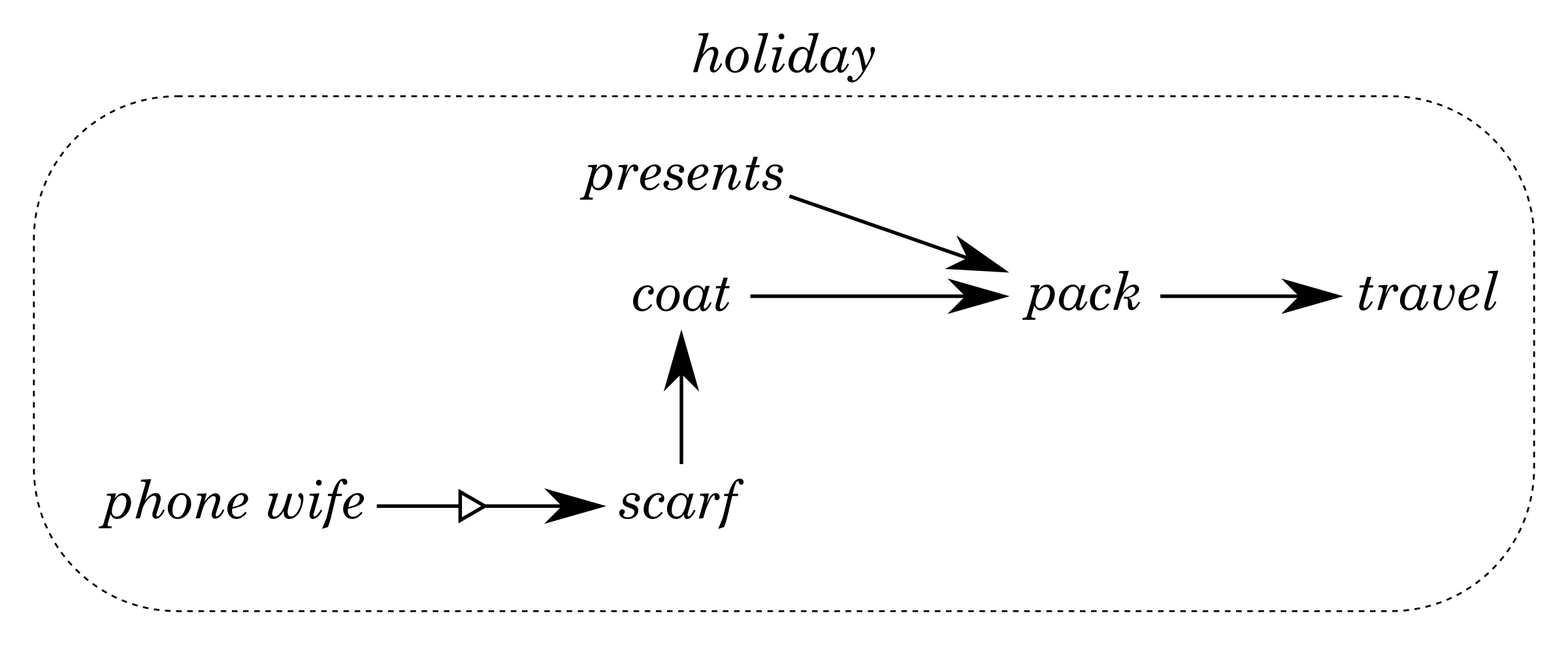
The graph is then linearised into a list of items by the todo function.
So, here you go: you can plan your holiday (or anything else) in Haskell using the alga library!
Constructing command lines in build systems
The above reminds me of build systems that construct command lines for executing various external programs, such as compilers, linkers, etc. A command line is just a list of strings, that typically include the path to the program that is being executed, paths to source files, and various configuration flags. Some of these strings may have order constraints between them, quite similar to todo lists. Let’s see if we can use our tiny DSL for todo lists for describing command lines.
Here is a simple command line to compile "src.c" with GCC compiler:
cmdLine1 :: Todo String cmdLine1 = "gcc" * ("-c" ~*~ "src.c" + "-o" ~*~ "src.o") λ> todo cmdLine1 Just ["gcc","-c","src.c","-o","src.o"]
Build systems are regularly refactored, and it is useful to track changes in a build system to automatically rebuild affected files if need be (for example, in the new GHC build system Hadrian we track changes in command lines and this helps a lot in its development). Some changes do not change the semantics of a build system and can therefore be safely ignored. As an example, one can rewrite cmdLine1 defined above by swapping the source and object file parts of the command line:
cmdLine2 :: Todo String cmdLine2 = "gcc" * ("-o" ~*~ "src.o" + "-c" ~*~ "src.c") λ> cmdLine1 == cmdLine2 True λ> todo cmdLine2 Just ["gcc","-c","src.c","-o","src.o"]
As you can see, the above change has no effect, as we would expect from the commutativity of +. Replacing ~*~ with the usual connect operator on the other hand sometimes leads to changes in the semantics:
cmdLine3 :: Todo String cmdLine3 = "gcc" * ("-c" * "src.c" + "-o" * "src.o") λ> cmdLine1 == cmdLine3 False λ> todo cmdLine3 Just ["gcc","-o","-c","src.c","src.o"]
The resulting sequence is correct from the point of view of a dependency graph, but is not a valid command line: the flag pairs got pushed apart. The change in semantics is recognised by the algebra and a rerun of the build system should reveal the error.
As a final exercise, let’s write a function that transforms command lines:
optimise :: Int -> Todo String -> Todo String optimise level = (* flag) where flag = vertex $ "-O" ++ show level λ> todo $ optimise 2 cmdLine1 Just ["gcc","-c","src.c","-o","src.o","-O2"]
As you can see, optimise 2 appends the optimisation flag "-O2" at the end of the command line, i.e. optimise 2 == (* "-O2").
Command lines in real build systems contain many conditional flags that are included only when compiling certain files on certain platforms, etc. You can read about how we deal with conditional flags in Hadrian here.
Under the hood
Scheduling a list of items subject to dependency constraints is a well-known problem, which is solved by topological sort of the underlying dependency graph. GHC’s containers library has an implementation of topological sort in Data.Graph module. It operates on adjacency lists and to reuse it we can define the following Graph instance:
newtype AdjacencyMap a = AM { adjacencyMap :: Map a (Set a) } deriving (Eq, Show) instance Ord a => Graph (AdjacencyMap a) where type Vertex (AdjacencyMap a) = a empty = AM $ Map.empty vertex x = AM $ Map.singleton x Set.empty overlay x y = AM $ Map.unionWith Set.union (adjacencyMap x) (adjacencyMap y) connect x y = AM $ Map.unionsWith Set.union [ adjacencyMap x, adjacencyMap y , fromSet (const . keysSet $ adjacencyMap y) (keysSet $ adjacencyMap x) ] adjacencyList :: AdjacencyMap a -> [(a, [a])] adjacencyList = map (fmap Set.toAscList) . Map.toAscList . adjacencyMap λ> adjacencyList $ clique [1..4] [(1,[2,3,4]),(2,[3,4]),(3,[4]),(4,[])]
Todo is built on top of the TopSort graph instance, which is just a newtype wrapper around AdjacencyMap based representation of graphs:
newtype TopSort a = TS { fromTopSort :: AdjacencyMap a } deriving (Show, Num) instance Ord a => Eq (TopSort a) where x == y = topSort x == topSort y
The custom Eq instance makes sure that graphs are considered equal if their topological sorts coincide. In particular all cyclic graphs fall into the same equivalence class corresponding to topSort g == Nothing:
λ> path [1..4] == (clique [1..4] :: TopSort Int) True λ> topSort $ clique [1..4] Just [1,2,3,4] λ> topSort $ path [1..4] Just [1,2,3,4] λ> topSort $ transpose $ clique [1..4] Just [4,3,2,1] λ> topSort $ circuit [1..4] Nothing
Function topSort simply calls Data.Graph.topSort performing the necessary plumbing, which is not particularly interesting.
The current implementation has two issues: the topological sort is not always lexicographically first, as evidenced by cmdLine3 above, where "-o" precedes "-c" in the final ordering. The second issue is that topSort does not satisfy the closure axiom defined in the previous blog post. One possible approach to fix this is to compute the transitive reduction of the underlying dependency graph before the topological sort.
Have a great holiday everyone!