After I got back from the holiday that I planned in the previous blog post, I spent the whole January playing with the algebra of graphs and trying to find interesting and useful ways of constructing graphs, focusing on writing polymorphic code that can manipulate graph expressions without turning them into concrete data structures. I’ve put together a small toolbox containing a few quirky types, which I’d like to share with you in this blog post. If you are not familiar with the algebra of graphs, please read the introductory blog post first.

Update: This series of blog posts was published as a functional pearl at the Haskell Symposium 2017.

Graph transpose

One of the simplest transformations one can apply to a graph is to flip the direction of all of its edges. It’s usually straightforward to implement but whatever data structure you use to represent graphs, you will spend at least O(1) time to modify it (say, by flipping the treatAsTransposed flag); much more often you will have to traverse the data structure and flip every edge, resulting in O(|V|+|E|) time complexity. What if I told you that by using Haskell’s type system, we can transpose polymorphic graphs in zero time? Sounds suspicious? Let’s see how this works.

Consider the following Graph instance:

newtype Transpose g = T { transpose :: g }

instance Graph g => Graph (Transpose g) where
    type Vertex (Transpose g) = Vertex g
    empty       = T empty
    vertex      = T . vertex
    overlay x y = T $ transpose x `overlay` transpose y
    connect x y = T $ transpose y `connect` transpose x -- flip

We wrap a graph in a newtype flipping the order of arguments to connect. Let’s check if this works:

λ> edgeList $ 1 * (2 + 3) * 4
[(1,2),(1,3),(1,4),(2,4),(3,4)]
λ> edgeList $ transpose $ 1 * (2 + 3) * 4
[(2,1),(3,1),(4,1),(4,2),(4,3)]

Cool! And this has zero runtime cost, because all we do is wrapping and unwrapping the newtype, which is guaranteed to be free. As an exercise, verify that transpose is an antihomomorphism on graphs, that is:

• T(ε) = ε
• T(v) = v
• T(x + y) = T(x) + T(y)
• T(x → y) = T(y) → T(x)

Furthermore, transpose is its own inverse: transpose . transpose = id.

To make sure transpose is only applied to polymorphic graphs, we do not export the constructor T, therefore the only way to call transpose is to give it a polymorphic argument and let the type inference interpret it as a value of type Transpose. The type signature is a little unsatisfying though:

λ> :t transpose
transpose :: Transpose g -> g

It’s not clear at all from the type that the function operates on graphs. Do you have any ideas how to improve it?

Merging graph vertices with a functor

Here is a puzzle for you: can you implement a function gmap that given a function a -> b and a polymorphic graph whose vertices are of type a will produce a polymorphic graph with vertices of type b by applying the function to each vertex? Yes, this is almost a Functor but it doesn’t have the usual type signature, because Graph is not a higher-kinded type.

My solution is as follows, but I feel there may be simpler ones:

newtype GraphFunctor a =
    GF { gfor :: forall g. Graph g => (a -> Vertex g) -> g }

instance Graph (GraphFunctor a) where
    type Vertex (GraphFunctor a) = a
    empty       = GF $ \_ -> empty
    vertex  x   = GF $ \f -> vertex (f x)
    overlay x y = GF $ \f -> gmap f x `overlay` gmap f y
    connect x y = GF $ \f -> gmap f x `connect` gmap f y

gmap :: Graph g => (a -> Vertex g) -> GraphFunctor a -> g
gmap = flip gfor

Essentially, we are defining another newtype wrapper, which pushes the given function all the way towards the vertices. This has no runtime cost, just as before, although the actual evaluation of the given function at each vertex will not be free, of course. Let’s test this!

λ> adjacencyList $ 1 * 2 * 3 + 4 * 5
[(1,[2,3]),(2,[3]),(3,[]),(4,[5]),(5,[])]
λ> :t gmap (+1) $ 1 * 2 * 3 + 4 * 5
gmap (+1) $ 1 * 2 * 3 + 4 * 5 :: (Graph g, Num (Vertex g)) => g
λ> adjacencyList $ gmap (+1) $ 1 * 2 * 3 + 4 * 5
[(2,[3,4]),(3,[4]),(4,[]),(5,[6]),(6,[])]

As you can see, we can increment the value of each vertex by mapping function (+1) over the graph. The resulting expression is a polymorphic graph, as desired. Again, we’ve done some useful work without turning the graph into a concrete data structure. As an exercise, show that gmap satisfies the functor laws: gmap id = id and gmap f . gmap g = gmap (f . g). A useful first step is to prove that mapping a function is a homomorphism:

•  M_f(ε) = ε
•  M_f(v) = f(v)
•  M_f(x + y) =  M_f(x) +  M_f(y)
•  M_f(x → y) =  M_f(x) → M_f(y)

An alert reader might wonder: what happens if the function maps two original vertices into the same one? They will be merged! Merging graph vertices is a useful function, so let’s define it in terms of gmap:

mergeVertices :: Graph g => (Vertex g -> Bool) -> Vertex g
    -> GraphFunctor (Vertex g) -> g
mergeVertices p v = gmap $ \u -> if p u then v else u

λ> adjacencyList $ mergeVertices odd 3 $ 1 * 2 * 3 + 4 * 5
[(2,[3]),(3,[2,3]),(4,[3])]

The function takes a predicate on graph vertices and a target vertex and maps all vertices satisfying the predicate into the target vertex, thereby merging them. In our example all odd vertices {1, 3, 5} are merged into 3, in particular creating the self-loop 3 → 3. Note: it takes linear time O(|g|) for mergeVertices to apply the predicate to each vertex (|g| is the size of the expression g), which may be much more efficient than merging vertices in a concrete data structure; for example, if the graph is represented by an adjacency matrix, it will likely be necessary to rebuild the resulting matrix from scratch, which takes O(|V|^2) time. Since for many graphs we have |g| = O(|V|), the matrix-based mergeVertices will run in O(|g|^2).

Expanding vertices into subgraphs (hey, monads!)

What do the operations of removing a vertex and splitting a vertex have in common? They both can be implemented by replacing each vertex of a graph with a (possibly empty) subgraph and flattening the result. Sounds familiar? You may recognise this as monad’s bind function, or Haskell’s operator >>=, which is so useful that it even made it to the Haskell’s logo. We are going to implement bind on graphs by wrapping it into yet another newtype:

newtype GraphMonad a =
    GM { bind :: forall g. Graph g => (a -> g) -> g }

instance Graph (GraphMonad a) where
    type Vertex (GraphMonad a) = a
    empty       = GM $ \_ -> empty
    vertex  x   = GM $ \f -> f x -- here is the trick!
    overlay x y = GM $ \f -> bind x f `overlay` bind y f
    connect x y = GM $ \f -> bind x f `connect` bind y f

As you can see, the implementation is almost identical to gmap: instead of wrapping the value f x into a vertex, we should just leave it as is. The resulting transformation is also a homomorphism. Let’s see how we can make use of this new type in our toolbox.

We are first going to implement a filter-like function induce that, given a vertex predicate and a graph, will compute the induced subgraph on the set of vertices that satisfy the predicate by turning all other vertices into empty subgraphs and flattening the result.

induce :: Graph g => (Vertex g -> Bool)
    -> GraphMonad (Vertex g) -> g
induce p g = bind g $ \v -> if p v then vertex v else empty

λ> edgeList $ clique [0..4]
[(0,1),(0,2),(0,3),(0,4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)]
λ> edgeList $ induce (<3) $ clique [0..4]
[(0,1),(0,2),(1,2)]
λ> induce (<3) (clique [0..4]) == (clique [0..2] :: Basic Int)
True

As you can see, by inducing a clique on a subset of the vertices that we like (<3), we get a smaller clique, as expected.

We can now implement removeVertex via induce:

removeVertex :: (Eq (Vertex g), Graph g) => Vertex g
    -> GraphMonad (Vertex g) -> g
removeVertex v = induce (/= v)

λ> adjacencyList $ removeVertex 2 $ 1 * (2 + 3)
[(1,[3]),(3,[])]

Removing an edge is not as simple. I suspect that this has something to do with the fact that the corresponding transformation doesn’t seem to be a homomorphism. Indeed, you will find it tricky to satisfy the last homomorphism requirement on R_x→y:

• R_x→y(x → y) = R_x→y(x) → R_x→y(y)

We can, however, implement a function disconnect that removes all edges between two different vertices as follows:

disconnect :: (Eq (Vertex g), Graph g) => Vertex g -> Vertex g
    -> GraphMonad (Vertex g) -> g
disconnect u v g = removeVertex u g `overlay` removeVertex v g

λ> adjacencyList $ disconnect 1 2 $ 1 * (2 + 3)
[(1,[3]),(2,[]),(3,[])]

That is, we create two graphs: one without u, the other without v, and overlay them, which removes both u → v and v → u edges. I still don’t have a solution for removing just a single edge u → v, or even just a self-loop v → v (note:  disconnect v v = removeVertex v). Maybe you can find a solution? (Update: Arseniy Alekseyev found a solution for removing self-loops that can be generalised for removing edges, see a note at the end of the blog post.)

Curiously, we can have a slightly shorter implementation of disconnect, because a function returning a graph can also be given a Graph instance:

instance Graph g => Graph (a -> g) where
    type Vertex (a -> g) = Vertex g
    empty       = pure empty
    vertex      = pure . vertex
    overlay x y = overlay <$> x <*> y
    connect x y = connect <$> x <*> y

disconnect :: (Eq (Vertex g), Graph g) => Vertex g -> Vertex g
    -> GraphMonad (Vertex g) -> g
disconnect u v = removeVertex u `overlay` removeVertex v

Finally, as promised, here is how we can split a vertex into a list of given vertices using the bind function:

splitVertex :: (Eq (Vertex g), Graph g) => Vertex g
    -> [Vertex g] -> GraphMonad (Vertex g) -> g
splitVertex v vs g = bind g $
    \u -> if u == v then vertices vs else vertex u

λ> adjacencyList $ splitVertex 1 [0, 1] $ 1 * (2 + 3)
[(0,[2,3]),(1,[2,3]),(2,[]),(3,[])]

Here vertex 1 is split into a pair of vertices {0, 1} that have the same connectivity.

Constructing De Bruijn graphs

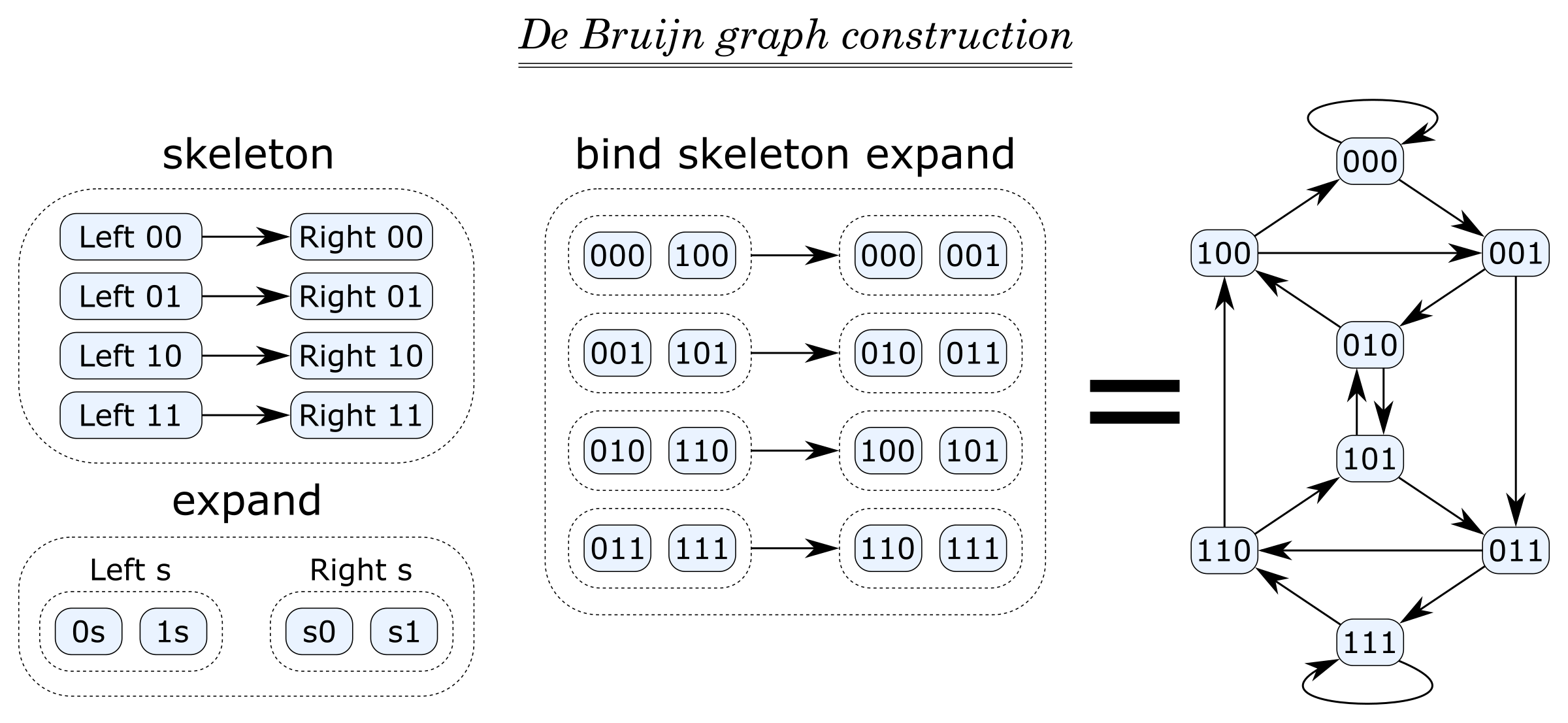
To demonstrate that we can construct reasonably sophisticated graphs using the presented toolkit, let’s try it on De Bruijn graphs, an interesting combinatorial object that frequently shows up in computer engineering and bioinformatics. My implementation is fairly short, but requires some explanation:

deBruijn :: (Graph g, Vertex g ~ [a]) => Int -> [a] -> g
deBruijn len alphabet = bind skeleton expand
  where
    overlaps = mapM (const alphabet) [2..len]
    skeleton = fromEdgeList [       (Left s, Right s)  | s <- overlaps ]
    expand v = vertices     [ either ([a]++) (++[a]) v | a <- alphabet ]

The function builds a De Bruijn graph of dimension len from symbols of the given alphabet. The vertices of the graph are all possible words of length len containing symbols of the alphabet, and two words are connected x → y whenever x and y match after we remove the first symbol of x and the last symbol of y (equivalently, when x = az and y = zb for some symbols a and b). An example of a 3-dimensional De Bruijn graph on the alphabet {0, 1} is shown in the diagram below (right).

Here are all the ingredients of the solution:

• overlaps contains all possible words of length len-1 that correspond to overlaps of connected vertices.
• skeleton is a graph with one edge per overlap, with Left and Right vertices acting as temporary placeholders (see the diagram).
• We replace a vertex Left s with a subgraph of two vertices {0s, 1s}, i.e. the vertices whose suffix is s. Symmetrically, Right s is replaced by a subgraph of two vertices {s0, s1}. This is captured by the function expand.
• The result is obtained by computing bind skeleton expand, as illustrated above.

…and this works as expected:

λ> edgeList $ deBruijn 3 "01"
[("000","000"),("000","001"),("001","010"),("001","011")
,("010","100"),("010","101"),("011","110"),("011","111")
,("100","000"),("100","001"),("101","010"),("101","011")
,("110","100"),("110","101"),("111","110"),("111","111")]
λ> all (\(x,y) -> drop 1 x == dropEnd 1 y) $ edgeList $ deBruijn 9 "abc"
True
λ> Set.size $ vertexSet $ deBruijn 9 "abc"
19683 -- i.e. 3^9

That’s all for now! I hope I’ve convinced you that you don’t necessarily need to operate on concrete data structures when constructing graphs. You can write both efficient and reusable code by using Haskell’s types for interpreting polymorphic graph expressions as maps, binds and other familiar transforms. Give me any old graph, and I’ll write you a new type to construct it! 😉

P.S.: The algebra of graphs is available in the alga library.

Update: Arseniy Alekseyev found a nice solution for removing self-loops. Let R_v denote the operation of removing a vertex v, and R_v→v denote the operation of removing a self-loop v → v. Then the latter can be defined as follows:

• R_v→v(ε) = ε
• R_v→v(x) = x
• R_v→v(x + y) = R_v→v(x) + R_v→v(y)
• R_v→v(x → y) = R_v(x) → R_v→v(y) + R_v→v(x) → R_v(y)

It’s not a homomorphism, but it seems to work. Cool! Furthermore, we can generalise the above and implement the operation R_u→v that removes an edge u → v:

• R_u→v(ε) = ε
• R_u→v(x) = x
• R_u→v(x + y) = R_u→v(x) + R_u→v(y)
• R_u→v(x → y) = R_u(x) → R_u→v(y) + R_u→v(x) → R_v(y)

Note that the size of the expression can substantially increase as a result of applying such operations. Given an expression g of size |g|, what is the worst possible size of the result |R_u→v(g)|?