Update: I have written a paper about selective applicative functors, and it completely supersedes this blog post (it also uses a slightly different notation). You should read the paper instead.
I often need a Haskell abstraction that supports conditions (like Monad) yet can still be statically analysed (like Applicative). In such cases people typically point to the Arrow class, more specifically ArrowChoice, but when I look it up, I find several type classes and a dozen of methods. Impressive, categorical but also quite heavy. Is there a more lightweight approach? In this blog post I’ll explore what I call selective applicative functors, which extend the Applicative type class with a single method that makes it possible to be selective about effects.
Please meet Selective:
class Applicative f => Selective f where handle :: f (Either a b) -> f (a -> b) -> f b
Think of handle as a selective function application: you apply a handler function of type a → b when given a value of type Left a, but can skip the handler (along with its effects) in the case of Right b. Intuitively, handle allows you to efficiently handle errors, i.e. perform the error-handling effects only when needed.
Note that you can write a function with this type signature using Applicative functors, but it will always execute the effect associated with the handler so it’s potentially less efficient:
handleA :: Applicative f => f (Either a b) -> f (a -> b) -> f b handleA x f = (\e f -> either f id e) <$> x <*> f
Selective is more powerful(*) than Applicative: you can recover the application operator <*> as follows (I’ll use the suffix S for Selective).
apS :: Selective f => f (a -> b) -> f a -> f b apS f x = handle (Left <$> f) (flip ($) <$> x)
Here we tag a given function a → b as an error and turn a value of type a into an error-handling function ($a), which simply applies itself to the error a → b yielding b as desired. We will later define laws for the Selective type class which will ensure that apS is a legal application operator <*>, i.e. that it satisfies the laws of the Applicative type class.
The select function is a natural generalisation of handle: instead of skipping one unnecessary effect, it selects which of the two given effectful functions to apply to a given value. It is possible to implement select in terms of handle, which is a good puzzle (try it!):
select :: Selective f => f (Either a b) -> f (a -> c) -> f (b -> c) -> f c select = ... -- Try to figure out the implementation!
Finally, any Monad is Selective:
handleM :: Monad f => f (Either a b) -> f (a -> b) -> f b handleM mx mf = do x <- mx case x of Left a -> fmap ($a) mf Right b -> pure b
Selective functors are sufficient for implementing many conditional constructs, which traditionally require the (more powerful) Monad type class. For example:
ifS :: Selective f => f Bool -> f a -> f a -> f a ifS i t e = select (bool (Right ()) (Left ()) <$> i) (const <$> t) (const <$> e)
Here we turn a Boolean value into Left () or Right () and then select an appropriate branch. Let’s try this function in a GHCi session:
λ> ifS (odd . read <$> getLine) (putStrLn "Odd") (putStrLn "Even") 0 Even λ> ifS (odd . read <$> getLine) (putStrLn "Odd") (putStrLn "Even") 1 Odd
As desired, only one of the two effectful functions is executed. Note that here f = IO with the default selective instance: handle = handleM.
Using ifS as a building block, we can implement other useful functions:
-- | Conditionally apply an effect. whenS :: Selective f => f Bool -> f () -> f () whenS x act = ifS x act (pure ()) -- | A lifted version of lazy Boolean OR. (<||>) :: Selective f => f Bool -> f Bool -> f Bool (<||>) a b = ifS a (pure True) b
See more examples in the repository. (Note: I recently renamed handle to select, and select to branch in the repository. Apologies for the confusion.)
Static analysis
Like applicative functors, selective functors can be analysed statically. As an example, consider the following useful data type Validation:
data Validation e a = Failure e | Success a deriving (Functor, Show) instance Semigroup e => Applicative (Validation e) where pure = Success Failure e1 <*> Failure e2 = Failure (e1 <> e2) Failure e1 <*> Success _ = Failure e1 Success _ <*> Failure e2 = Failure e2 Success f <*> Success a = Success (f a) instance Semigroup e => Selective (Validation e) where handle (Success (Right b)) _ = Success b handle (Success (Left a)) f = Success ($a) <*> f handle (Failure e ) _ = Failure e
This data type is used for validating complex data: if reading one or more fields has failed, all errors are accumulated (using the operator <> from the semigroup e) to be reported together. By defining the Selective instance, we can now validate data with conditions. Below we define a function to construct a Shape (a Circle or a Rectangle) given a choice of the shape s :: f Bool and the shape’s parameters (Radius, Width and Height) in an arbitrary selective context f.
type Radius = Int type Width = Int type Height = Int data Shape = Circle Radius | Rectangle Width Height deriving Show shape :: Selective f => f Bool -> f Radius -> f Width -> f Height -> f Shape shape s r w h = ifS s (Circle <$> r) (Rectangle <$> w <*> h)
We choose f = Validation [String] to report the errors that occurred when reading values. Let’s see how it works.
λ> shape (Success True) (Success 10) (Failure ["no width"]) (Failure ["no height"]) Success (Circle 10) λ> shape (Success False) (Failure ["no radius"]) (Success 20) (Success 30) Success (Rectangle 20 30) λ> shape (Success False) (Failure ["no radius"]) (Success 20) (Failure ["no height"]) Failure ["no height"] λ> shape (Success False) (Failure ["no radius"]) (Failure ["no width"]) (Failure ["no height"]) Failure ["no width","no height"] λ> shape (Failure ["no choice"]) (Failure ["no radius"]) (Success 20) (Failure ["no height"]) Failure ["no choice"]
In the last example, since we failed to parse which shape has been chosen, we do not report any subsequent errors. But it doesn’t mean we are short-circuiting the validation. We will continue accumulating errors as soon as we get out of the opaque conditional:
twoShapes :: Selective f => f Shape -> f Shape -> f (Shape, Shape) twoShapes s1 s2 = (,) <$> s1 <*> s2 λ> s1 = shape (Failure ["no choice 1"]) (Failure ["no radius 1"]) (Success 20) (Failure ["no height 1"]) λ> s2 = shape (Success False) (Failure ["no radius 2"]) (Success 20) (Failure ["no height 2"]) λ> twoShapes s1 s2 Failure ["no choice 1","no height 2"]
Another example of static analysis of selective functors is the Task abstraction from the previous blog post.
instance Monoid m => Selective (Const m) where handle = handleA type Task c k v = forall f. c f => (k -> f v) -> k -> Maybe (f v) dependencies :: Task Selective k v -> k -> [k] dependencies task key = case task (\k -> Const [k]) key of Nothing -> [] Just (Const ks) -> ks
The definition of the Selective instance for the Const functor simply falls back to the applicative handleA, which allows us to extract the static structure of any selective computation very similarly to how this is done with applicative computations. In particular, the function dependencies returns an approximation of dependencies of a given key: instead of ignoring opaque conditional statements as in Validation, we choose to inspect both branches collecting dependencies from both of them.
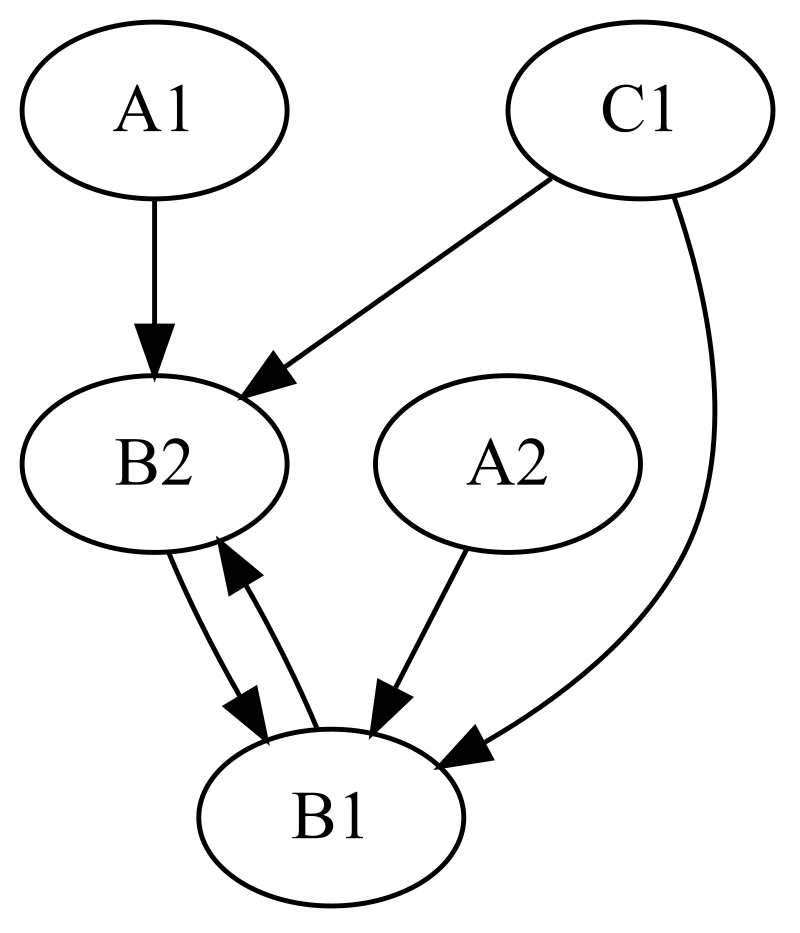
Here is an example from the Task blog post, where we used the Monad abstraction to express a spreadsheet with two formulas: B1 = IF(C1=1,B2,A2) and B2 = IF(C1=1,A1,B1).
task :: Task Monad String Integer task fetch "B1" = Just $ do c1 <- fetch "C1" if c1 == 1 then fetch "B2" else fetch "A2" task fetch "B2" = Just $ do c1 <- fetch "C1" if c1 == 1 then fetch "A1" else fetch "B1" task _ _ = Nothing
Since this task description is monadic we could not analyse it statically. But now we can! All we need to do is rewrite it using Selective:
task :: Task Selective String Integer task fetch "B1" = Just $ ifS ((1==) <$> fetch "C1") (fetch "B2") (fetch "A2") task fetch "B2" = Just $ ifS ((1==) <$> fetch "C1") (fetch "A1") (fetch "B1") task _ _ = Nothing
We can now apply the function dependencies defined above and draw the dependency graph using your favourite graph library:
λ> dependencies task "B1" ["A2","B2","C1"] λ> dependencies task "B2" ["A1","B1","C1"] λ> dependencies task "A1" [] λ> writeFile "task.dot" $ exportAsIs $ graph (dependencies task) "B1" λ> :! dot -Tsvg task.dot -o task.svg
This produces the graph below, which matches the one I had to draw manually last time, since I had no Selective to help me.
Laws
Instances of the Selective type class must satisfy a few laws to make it possible to refactor selective computations. These laws also allow us to establish a formal relation with the Applicative and Monad type classes. The laws are complex, but I couldn’t figure out how to simplify them. Please let me know if you find an improvement.
- (F1) Apply a pure function to the result:
f <$> handle x y = handle (second f <$> x) ((f .) <$> y)
- (F2) Apply a pure function to the left (error) branch:
handle (first f <$> x) y = handle x ((. f) <$> y)
- (F3) Apply a pure function to the handler:
handle x (f <$> y) = handle (first (flip f) <$> x) (flip ($) <$> y)
- (P1) Apply a pure handler:
handle x (pure y) = either y id <$> x
- (P2) Handle a pure error:
handle (pure (Left x)) y = ($x) <$> y
- (A1) Associativity (in disguise):
handle x (handle y z) = handle (handle (f <$> x) (g <$> y)) (h <$> z) where f x = Right <$> x g y = \a -> bimap (,a) ($a) y h z = uncurry z -- or in operator form with (<*?) = handle x <*? (y <*? z) = (f <$> x) <*? (g <$> y) <*? (h <$> z)
Note that there is no law for handling a pure value, i.e. we do not require that the following holds:
handle (pure (Right x)) y = pure x
In particular, the following is allowed too:
handle (pure (Right x)) y = const x <$> y
We therefore allow handle to be selective about effects in this case. If we insisted on adding the first version of the above law, that would rule out the useful Const instance. If we insisted on the second version of the law, we would essentially be back to Applicative.
A consequence of the above laws is that apS satisfies Applicative laws (I do not have a formal proof, but you can find some proof sketches here). Note that we choose not to require that apS = <*>, since this forbids some interesting instances, such as Validation defined above.
If f is also a Monad, we require that handle = handleM.
Using the laws, it is possible to rewrite any selective computation into a normal form (the operator + denotes the sum type constructor):
f (a + b + ... + z) -- An initial value of a sum type -> f (a -> (b + ... + z)) -- How to handle a's -> f (b -> (c + ... + z)) -- How to handle b's ... -> f (y -> z) -- How to handle y's -> f z -- The result
In words, we start with a sum type and handle each alternative in turn, possibly skipping unnecessary handlers, until we end up with a resulting value.
Alternative formulations
There are other ways of expressing selective functors in Haskell and most of them are compositions of applicative functors and the Either monad. Below I list a few examples. All of them are required to perform effects from left to right.
-- Composition of Applicative and Either monad class Applicative f => SelectiveA f where (|*|) :: f (Either e (a -> b)) -> f (Either e a) -> f (Either e b) -- Composition of Starry and Either monad -- See: https://duplode.github.io/posts/applicative-archery.html class Applicative f => SelectiveS f where (|.|) :: f (Either e (b -> c)) -> f (Either e (a -> b)) -> f (Either e (a -> c)) -- Composition of Monoidal and Either monad -- See: http://blog.ezyang.com/2012/08/applicative-functors/ class Applicative f => SelectiveM f where (|**|) :: f (Either e a) -> f (Either e b) -> f (Either e (a, b))
I believe these formulations are equivalent to Selective, but I have not proved the equivalence formally. I like the minimalistic definition of the type class based on handle, but the above alternatives are worth consideration too. In particular, SelectiveS has a much nicer associativity law, which is just (x |.| y) |.| z = x |.| (y |.| z).
Concluding remarks
Selective functors are powerful: like monads they allows us to inspect values in an effectful context. Many monadic computations can therefore be rewritten using the Selective type class. Many, but not all! Crucially, selective functors cannot implement the function join:
join :: Selective f => f (f a) -> f a join = ... -- This puzzle has no solution, better solve 'select'!
I’ve been playing with selective functors for a few weeks, and I have to admit that they are very difficult to work with. Pretty much all selective combinators involve mind-bending manipulations of Lefts and Rights, with careful consideration of which effects are necessary. I hope all this complexity can be hidden in a library.
I haven’t yet looked into performance issues, but it is quite likely that it will be necessary to add more methods to the type class, so that their default implementations can be replaced with more efficient ones on instance-by-instance basis (similar optimisations are done with Monad and Applicative).
Have you come across selective functors before? The definition of the type class is very simple, so somebody must have looked at it earlier.
Also, do you have any other interesting use-cases for selective functors?
Big thanks to Arseniy Alekseyev, Ulan Degenbaev and Georgy Lukyanov for useful discussions, which led to this blog post.
Footnotes and updates
(*) As rightly pointed out by Darwin226 in the reddit discussion, handle = handleA gives a valid Selective instance for any Applicative, therefore calling it less powerful may be questionable. However, I would like to claim that Selective does provide additional power: it gives us vocabulary to talk about unnecessary effects. We might want to be able to express three different ideas:
- Express the requirement that all effects must be performed. This corresponds to the Applicative type class and handleA. There is no way to distinguish necessary effects from unnecessary ones in the Applicative setting.
- Express the requirement that unnecessary effects must be skipped. This is a stricter version of Selective, which corresponds to handleM.
- Express the requirement that unnecessary effects may be skipped. This is the version of Selective presented in this blog post: handle is allowed to be anywhere in the range from handleA to handleM.
I think all three ideas are useful, and it is very interesting to study the stricter version of Selective too. I’d be interested in hearing suggestions for the corresponding set of laws. The following two laws seem sensible:
handle (Left <$> x) f = flip ($) <$> x <*> f handle (Right <$> x) f = x
I still don’t get why do we need that typeclass.
“`
handle :: Applicative f => f (Either a b) -> f (a -> b) -> f b
handle f fa = bimap f id fa
“`
Look: no new typeclasses! The `Selective` doesn’t even narrow anything, as any `Applicative` can do it.
It just uses standart `Bifunctor (Either e a)` instance.
There was an $lt;$$gt; between “id” and “fa”. What is the syntax for code blocks here?
Is this what you meant? I inserted `fmap` as you suggest in your second comment (yes, this blog engine is annoying in terms of code blocks).
handle :: Applicative f => f (Either a b) -> f (a -> b) -> f b
handle f fa = fmap (bimap f id) fa
This doesn’t type check. Feel free to link to a GitHub gist where we could continue the discussion with code highlighting.
I think one can make it work in two ways:
* By eventually rewriting your code into `handleA`, which is in the blog post. But then when you have got a `Right b`, you don’t need the handler effect and would like to skip it, but the Applicative interface doesn’t allow you to do that.
* You could also use `join` to collapse `f (f b)` into `f b`. But that requires a monad, hence, being equivalent to `handleM`.
Hope this clarifies things!
Hi there. A friend and I were discussing this, and came upon the suspicion that this is basically saying `handle :: (Functor f, Monad (EitherT b f)) => f (Either a b) -> f (a -> b) -> f b`.
This stuff gets a little awkward to express in Haskell because instance dictionaries aren’t explicit and overlap is a nono, but I think the `Validation` stuff is also a monad instance for `EitherT (Validation e) b`s. I’ve put some experimentation along these lines in a gist here:
https://gist.github.com/masaeedu/ca3cdd13fd83422601ac0cc32dd7714d
Hey! Thanks for sharing an interesting alternative encoding. Are you sure this instance is lawful?
instance {-# OVERLAPS #-} Monad (EitherT b (Validation e))
My feeling is that the line below breaks the `ap` law
EitherT (Failure e) >>= _ = EitherT (Failure e)
since the behaviour is different from the underlying Applicative instance.
Hi @Andrey. It breaks the laws if you compare `ap` to the “ given in the instance `instance Semigroup e => Applicative (Validation e)`. However we have two independent instances of applicative for `Validation`, and for the second one we have by definition `() = ap`. The multiple instances of applicative is why we run into issues with overlap.
Under some hypothetical world with [scrap your typeclasses](http://www.haskellforall.com/2012/05/scrap-your-type-classes.html) we could have multiple instances of a class for the same datatype without even the need for newtype wrappers like `EitherT`. In such circumstances you’d again unambiguously see the “ derived from the monad to be identical to the monad’s `ap`, and the “ from Validation’s standard applicative instance to be some other thing.
In theory I don’t think is not a problem; after all we don’t expect the empty for `IntProduct` to obey the laws with respect to `IntSum`’s `mappend`. In practice, this means your encoding is much more idiomatic haskell.
I’m afraid my usage of the spaceship operator disappeared (maybe it was interpreted as an HTML tag). Hopefully the meaning is still roughly clear?
Thanks Asad! Yes, it’s all clear. It’s a cool encoding, I had to play with it on a few examples to really believe it works 🙂 And it does!