In the simple example of connecting a charged capacitor to a self-timed switching circuit, say a ring oscillator (Fig.1)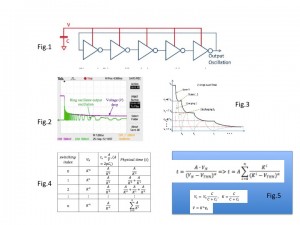
we have the process of discharging the cap shown in Fig. 2 (this is taken from the testing of the real silicon – 180nm CMOS). A simple mathematical analysis of this behaviour considers the discretisation, shown in Fig. 3 and 4, which is captured by the hyperbola function in Fig. 5 for V vs time (if we only look at the super-threshold region of the transistors in the inverters). Here K is a ratio of charge sharing between the main cap and a small parasitic cap that is charged at every step of the switching process in the ring chain. A is a constant determined by the inherent parameters of the transistors in the inverters in the oscillator.
One can generalise this analysis to considering a situation with a capacitive source of energy and an arbitrary asynchronous circuit being powered by such a cap. The math characetrisation of such systems will involve use of power laws. Indeed, a simple huperbola described by y=a/x is already a power law. Consider x and y both in log scale, this will be log(y)=log(a)-log(x), which is a straight descending slope lifted up to log(a).
My conjecture is that most of the processes in biology (such a development of biogradients from concentrations of nutrient molecules), economics (bank accounts being debited by its users) etc., they all fit similar patterns. So, isn’t the system of caps and async switching circuits an adequate computational paradigm (and a new type of computers!) for many processes in real life?