There is a lot of resistance amongst engineers and scientists to believing that the physics of electromagnetic signals and dynamic processes involving such signals is NOT based on sine waves. There is so much in engineering that has been and is still being invested into the mathematics and tools supporting harmonics based analytics and design activities of thousands of engineers. Equally, thousands of academics are teaching hundreds of thousands of electrical engineering students all this on and on.
But let’s think what we can learn from nature that communicates signals from one point in space to another point and does it in a most frugal and at the same time prodigal way.
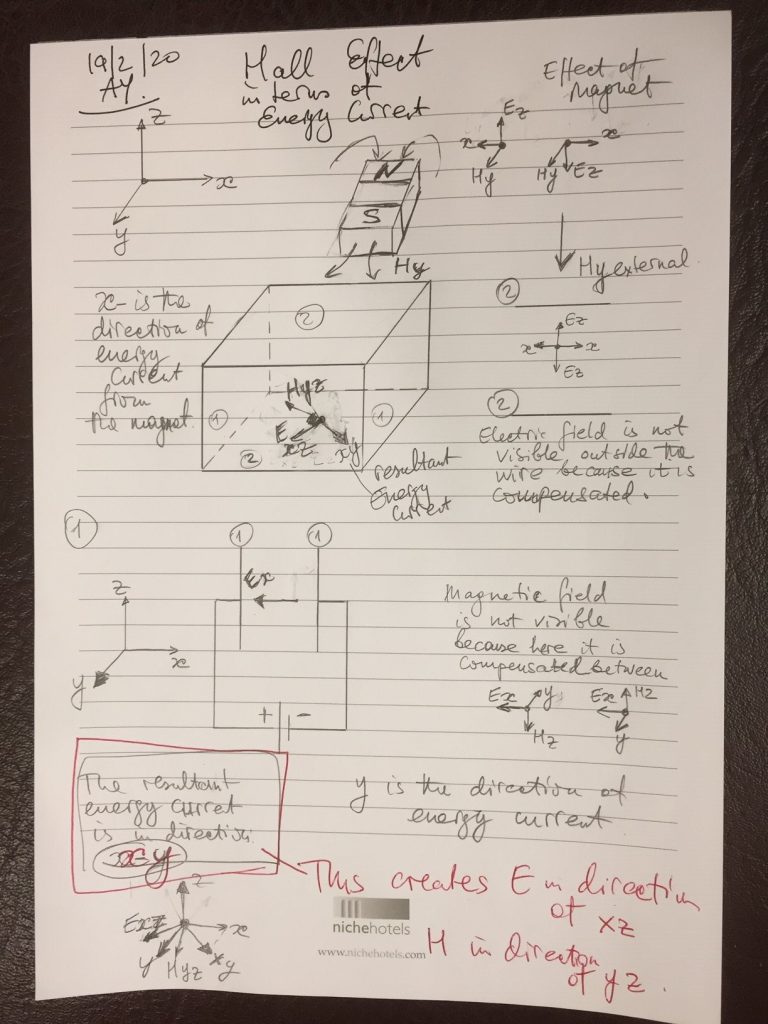
Imagine that we need to send a signalling event from point A to point B in space. This clearly involves some sort of motion. What kinds of motions we know. Well, at least two. One directional – that would be, for our example, moving along a straight line between A and B. Another type of motion we know rotational. This latter one should go if there is a point in the circle or sphere around which the notion can revolve. So, if the signal event involves the change in say electric field E and magnetic field H, we know that their vector product ExH forms Poynting vector, which shows the direction of the signal propagation. This propagation can only happen at speed of light in the medium (as there has been no evidence of otherwise!). If the direction of the vectors E and H is not changing in time at point A, our signal, defined by the Poynting vector ExH, will travel from point A to point B directly, albeit, this direction may not be straight line as it may be determined by the surrounding environment’s properties of epsilon and mu. So, for example if that environment is a transmission line (TL) formed by two metallic plates, then the Poynting vector will travel in the direction defined by the TL.
Now, if E and H elements of the vector are steps, then clearly these steps will form pulses, both in time and space. Now if for example these components of the vector are themselves in the rotational motion, and this rotation of E and H happens with a particular frequency omega, then the phase of the rotation omega*time will form an instantaneous value of the angle whose sine and cosine will determine the value of the potential produced, say, by the E component, between the plates of the TL. Unfold this rotation of vector E in space in the direction of the propagation of the Poyning vector, and you get a spiral – which is a superposition of the rotational and directional motions. The projection of this spiral on the normal plane along the Poynting vector’s direction will give us a sine-wave for E, likewise a cosine-wave for H. Hence rotational shift of 90 degrees will manifest itself as a longitudal phase shift of 90 degrees.
So, to summarise, the sine-wave is a product of a combined effect of a rotational motion and longitudal motion. But what’s important is that this sine-wave has a clear point of the start and end, and it’s not being there as a fundamental element. It is a mathematical trace of the superposition of fundamental elements of motion.
Another possible source of sine-waves is a successive oscillation of step-wise process in the longitudal direction, between two points. This is something that we have already discussed in earlier blogs, where we talked about the physical processes of propagation of energy current in transmission lines. Indeed if we connect a TL which has an open circuit end with the TL which is short circuited end, we have the effect of C and L combined, and the process of reflection of the energy current in this system, will form a series of steps which can be approximated by a sine-wave. Again, the sin-wave is a mathematical product of more primitive physical process.
In my recent email exchange with a group of people arguing with Ivor Catt about the primal nature of sine-waves, I wrote:
“Mechanics tells us there are two basic motion types. Direct and rotation around a point. If we assume that ExH can follow both, the latter for example, under the influence of another force (gravity?), can help us the express the effect of “corkscrew propagation”, and hence spatio temporal sinewaves. Actually a corkscrew or spiral is a good explanation of an AC shaped energy current around a wire. Light can propagate from its source in myriads of corkscrews by the way! ”
“By the way a corkscrew-like propagation of signal (hence, information) via a medium with natural resistance or friction (usual epsilon and mu properties) would be most effective, again from mechanical analogy point of view. Nature, again, following Occam’s razor principle, would do it the same way we penetrate into a cork or a wall, and that’s what nature would always do if it needs to pass information from one point to another! Energy current screws up everything! Ha-ha!”
I also recommend to someone who wishes to visualise these corkscrew processes to have a look at these wonderful videos on youtube:
https://www.youtube.com/watch?v=WCxXPTtQFm4
https://www.youtube.com/watch?v=0jHsq36_NTU