Category Archives: Energetic Computing

Discussion with Dave Walton about the nature and size of photon

Posted on by
Reply

About a year or so ago, I had an interesting email exchange with Dave Walton about photon size and how photon can be seen as a form of energy current extracted from an atom, much like a pulse or pulse train is generated when we discharge a capacitor …

Herein I am reproducing our exchange:

Alex Yakovlev:

https://www.electronicsweekly.com/news/business/surrey-university-changes-understanding-lasers-2020-07/?eea=NmZ5MUlzVG9HQ2ZyeldVM0E2TC9TR1Mvc1BsczNWd0pKM2lhSU5rMFNBTT0=&n_hash=1282&utm_source=e-shot&utm_medium=email&utm_campaign=EW-6012-(Edi)DailyNewsletter-%231282

An example of the demonstration that quantum physics is NOT the way to explain physics. Here is a story about lasers from Electronics Weekly:

+++++++++++++++++++++++++++++++++++
“Markus Pollnau, Professor in Photonics at the University of Surrey, said: “Since the laser was invented in 1960, the laser spectral linewidth has been treated as the stepchild in the descriptions of lasers in textbooks and university teaching worldwide, because its quantum-physical explanation has placed extraordinary challenges even for the lecturers.

“As we have explained in this study, there is a simple, easy-to-understand derivation of the laser spectral linewidth, and the underlying classical physics proves the quantum-physics attempt of explaining the laser spectral linewidth hopelessly incorrect. This result has fundamental consequences for quantum physics.””

++++++++++++++++++++++++++++++++++

Dave Walton:

I have puzzled for some time over two simple questions:

1.  How long is a photon?

2.  Why is the wavelength of light so much longer than the physical size of an atom.

As far as question 1 is concerned, the authors of this paper seem to be seeing the photon as a truncated sine wave which leads to its finite spectral width when expressed as a Fourier transform.  This can lead directly to a calculation of photon length.

Question 2 is a puzzle to me.  As engineers we are familiar that the size of an effective antenna must be of the order of the radiated wavelength.  (1/4 wave or 5/8 wave etc).  But the atom is much smaller than the wavelength of emitted light.  The type size of an atom is 5×10^-10 m, but the wavelength of light is of the order of 5 x 10^-7 m, which is a factor of 1000 times larger.  So how does it succeed in being such an efficient radiator?

Of course, Quantum Theory does not address these questions at all.  It simply states that the ‘Quantum Jump’ happens, and we cannot dissect it any further.

Alex Yakovlev:

I like both of your questions a lot.

Questions about real physical size dimensions are most pertinent if we think about energy current propagating in space (but how else to think?!).

Quantum Theory does not seem to address the dynamics of energy in real space, succumbing to abstract transitions between states in phase (state) space.

Reading your points regarding these questions is fascinating. Re: Q2, in particular, it begs for something like the sine wave period (i.e., wavelength) can only be 1000 longer than the atom IFF this sine wave is constructed of many (order of 1000 or so) steps, each the size of the atom, and each such step is the time of flight of the ExH current travelling between the ‘walls of the atom’. Pretty much like we have the time constant of the capacitor charge (discharge) exponential via resistor R, where the cap is a TL.

Isn’t it?

So, generally all these different wavelengths, can they be the result of the epsilon/mu (i.e. characteristic impedance of the medium) plus sizes of the unit of space that generates the light producing the sine wave in a manner similar to an L&C TL?

And photon is indeed a section of that sine wave.

I reproduced in my RS paper [cf. Energy current and computing | Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences (royalsocietypublishing.org)] your derivation of the time constant for the exponential charge/discharge of the stepwise processes, i.e., tau= eps*l*R/f, where l is the TL length, f is a geometric parameter linking the unit cap f=eps/c.

Perhaps, we can derive the period of the sine wave for the case of the L&C pair of TL? and this way determine the length of photon?

Dave Walton:

Very Interesting Alex.

It is amazing how the obvious can escape one for so long, but I had honestly never considered a transmission line model for the atom (!!).

Given the factor of 1,000 between the atomic diameter and the wavelength of the photon, this would suggest about 1000 transitions before all of the energy current escapes.  This suggests a reflection coefficient of the same order, i.e., 1/1000.

The next questions would seem to be, 

1.  What is the energy current arrangement in the atom?

2.  How exactly do these arrangements change during the process of emission?

I would be very interested to hear your thoughts on these and other issues which arise.

Alex Yakovlev:

Just to clarify, if we have 1000 steps for one swing of the wave (or exponential) between High and Low, should not the reflection be a complement, i.e., 999/1000.

That is basically to say that the characteristic impedance of the internals of the atom is 1000 times smaller than the ohmic impedance of the interface, right?

For comparison, Fig. 10 of Forrest’s paper 

http://www.naturalphilosophy.org//pdf//abstracts/abstracts_6554.pdf

Shows quite an opposite effect where the TL is so long that the time of flight in TL is twice that of the time constant of the equivalent RC circuit. Here, despite the fact that the reflection coefficient is even negative, the step is commensurate with the time constant. So, this is probably the effect of the capacitance of the TL being relatively small.

So, we somehow, need to take into account not only the Z0 vs R ratios, but also C as a function of the length and epsilon, which in the atomic case needs to be relatively large compared to ordinary coax like TLs. For the atom, we probably talk about much higher C per size unit, i.e., very high epsilon, right?

Incidentally, can we also calculate the frequency/clock period of the TL-based LC circuit? Was it your or Mike Gibson’s derivation of the sinewave for the TL-based LC oscillator? In Ivor’s Electromagnetics 1 book, I cannot find the frequency-period parameters of the sine wave, so we could work out some likely L and C values for the atom.

Your Qs:

1.  What is the energy current arrangement in the atom?

That is a good question. If we think about 3D this might be some kind of cube with the Poynting vector rotating around the nucleus, with E directed radially and H azimuthally?

2.  How exactly do these arrangements change during the process of emission?

What would trigger emission? some sort of window opening so that the sine wave will be radiate out?

Alex Yakovlev, continued:

Just played a bit with numbers.

Suppose we play with a cap model of the atom, and we’d like to find the length unit C, bearing in mind that the exponential’s time constant tau should be 1000 that of the step.

The key equation is

RC*l = 1000*l/c

R is the resistance of discharge

C is unit length cap

l is length

c is speed of light in the medium, let’s say 2*10^8 m/s

eliminating l, we have

RC=1000/c,

suppose R=1000Ohm.

We have C=1/c=5nF/m

Does it sound reasonable?

Suppose we use the parallel plate cap model:

C=eps*(w/a), where w is width and a is distance between the plates.

What should they be? 

Suppose the ratio between w and a, w/a is 5000.

This means that our eps then must be 10^(-12), does it sound realistic?

In vacuo, I think eps0 is about that order, 8.85*10^(-12).

Dave Walton:

Yes, the numbers do seem reasonable, but would you agree that the real challenge is to understand (or at least model) how the energy current distribution changes when a photon is emitted.  This should ultimately lead to the undemanding of the probability distribution in the orbitals.

This is tough.

Alex Yakovlev:

Dave,

This is puzzling.

Assuming that the atom is an LC loop with distributed parameters and a normally closed door, then it emits a photon in the form of an exponential/sine wave section. What then happens? My knowledge of atomic physics is rusty and weak. But presumably the aperture and interval of door opening depends on some external factors, right?

It’s a bit like we control the switch (externally) for a TL when the energy current comes out during the discharge process. Can we extract energy from Capacitive or LC-ive by portions – sections of exponential or chunks of sine wave?

I am pretty sure there should be a deterministic model – or at least one based on some sort of histograms of frequencies of spending time in different states – rather than purely stochastic probability model.

On a slightly different yet related side:

It seems that with energy current trapped in units like atoms or TLs, we have to deal with the two levels of dynamics:

1) higher frequency one – which is concerned with the vacillating TEM inside the atom or TL – basically where the step or period is determined by the eps and mu parameters and the geometry of the atom/TL

2) lower frequency one – which is concerned with some macro-elements – like resistors and switches that are controlled outside – these are parameters like time constants of charge/discharge exponentials or periods of sine waves.

Interestingly, that (1) is about the level of 100s of THz – that close to infrared and higher frequency light – people seem to know how to sense it at the level of photonic materials

(2) is the modern analogue electronics – with lumped LC loop antennas – somewhere up to 100 GHz. 

What’s between is some sort of dead zone – a gap (between materials level and circuits level), where not much can be done. 

This is my own perception, maybe I am wrong. I wonder what you think about it.

On ohmic losses in caps and transmission lines

Posted on by
Reply

Some people object the idea of reciprocating ExH waves in a charged capacitor because they claim that then we should have ohmic losses. Why?

Why should we associate the emergence of ohmic losses with the basic ExH energy current propagation. At this level there is no point to talk about ohmic losses because at this level we have no idea about any charge movement, i.e. no electric current is defined here. It’s all about EM energy current.
Ohmic losses need only be considered at the level of the superposition of Electric and Magnetic fields, i.e. at the level of V and I values in a particular place in space and a particular point in time.
If we take any of Wakefield experiments, we can find in them an interval of time at a certain place where the odds of overlap of two reciprocating waves are such that they produce no current (i.e. the cumulative effect on magnetic field is zero), so there are ohmic losses here and then. This does not however preclude the two ExH waves to move in opposite directions.

The real sense of energy conservation law is in permanent and omnipresent motion of energy

Posted on by
Reply

In my email exchange with Ivor Catt, a following idea came to my mind.

The law of energy conservation as it is being presented to students and understood is rather abstract as it begs for many interpretations, because energy exists in its permanent and omnipresent motion. Even if it is trapped in a fragment of space like a capacitor or an elementary particle it is in motion. 


So, what seems to be less convoluted is the law that energy can only exist in motion and it can only move at speed of light. That’s actually what conservation of energy is. This is true by Occam’s razor principle and does not need to be proven. So, it is necessarily so before or after the switch [between voltage source and a capacitor] is closed … and without this law we would not have had those prefect contrapuntal effects, including those that ’cause’ people to think we have stationary conditions in capacitors and transmission lines.

Static vs Dynamic and Charges vs Fields

Posted on by
Reply

There is a constant debate in Electromagnetism between the Charge-based views and Field-based views. I am of course over-simplifying the picture here, at least terminologically. But the main point is that you can talk about EM either from the point of view of; (i) objects that have mass, like electrons, protons, ions etc – I called them collectively charges or charge carriers, or (ii) entities that carry EM energy, like strength of electric and magnetic field, Poyinting vector etc – those are not associated with mass. Both views are often linked to some form of motion, or dynamics. For the world of objects people talk about moving charges, electric current, static charges etc. For the world of fields, people talk about EM waves, TE, TM and TEM, energy current, static field etc.

Often people talk about a mix of both views, and that’s where many paradoxes and contradictions happen. For example, there is an interesting ‘puzzle’ that has been posed to the world by Ivor Catt. It is sometimes called Catt’s question or Catt Anomaly.

http://www.electromagnetism.demon.co.uk/cattq.htm

Basically, the question is about: when a step in voltage is transmitted in a transmission line from a source to the end, according to the classical EM theory charge appears on both wires (+ on the leading wire, and – on the grounded wire): Where does this new charge come from?

Surprisingly, there has not been a convincing answer from anyone that would not violate one or another aspect of the classical EM theory.

Similar to this, there is a challenge posed by Malcolm Davidson, called Heaviside Challenge https://www.oliver-heaviside.com/ that hasn’t also been given a consistent response even though the challenge has been posed with a 5 thousand USD prize!

So it seems that there is a fundamental problem in reconciling the two worlds, in a consistent theory based on physical principles and laws, rather than mathematical abstractions.

However, there is a hope that with the way to understand and explain EM phenomena, especially in high-speed electronic circuits, is through the notion of a Heaviside signal and the principle of energy-current (Poyinting vector) that never ceases from travelling with the speed of light in the medium. In terms of energy current perfect dielectrics are perfect conductors of energy, whereas perfect charge conductors are perfect insulators for EM energy current.

So, while those who prefer the charge based view of the world may continue to talk about static and dynamic charges, those who see the world via energy current live in the world where there is no such a thing as static electric or magnetic field, because TEM signal can only exist in motion with a speed of light in the medium. Medium is characterised by its permittivity and permissibility and gives rise to two principal parameters – speed of light and characteristic impedance. The inherent necessity of the TEM signal to move is stipulated by Galileo/Newton’s principles of geometric proportionality, which effectively define the relations between any change of the field parameter in time with its change in space. Those two changes are linked fundamentally, hence we have the coefficient of proportionality delta_x/delta_t, also known as speed of light, which gives rise to causality between the propagation of energy or information and momenta of force acting on objects with mass.

Another consequence of the ever-moving energy current is its ability to be trapped in a segment of space, pretty much what we can have in a so called capacitor, and thus form an energized fragment of space, that gives rise to an object with mass, e.g. a charged particle such as an electron. So, this corollary of the first principle of energy current paves the way to the view of EM that is based on charged particles.

The Heaviside Prize

Posted on by
Reply

Last weekend I twitted on the following exciting challenge:

The Heaviside Prize:

https://youtube.com/watch?v=mr9-Nu5HvWM&feature=youtu.be…

$5000 for someone who will explain the physical reality (without using maths!) of the electric current when a digital step propagates in USB-like transmission line. Students, engineers, academics, tackle this challenge!!!

Correction on my previous blog and some interesting implications …

Posted on by
Reply

Andrey Mokhov spotted that to satisfy the actual inverse Pythagorean we need to have alpha=1/2 rather than 2. That’s right. Indeed, what happens is that if we have alpha = 1/2 we would have (1/a)^2=(1/a1)^2+(1/a2)^2. This is what the inverse Pythagorean requires. In that case, for instance if a1=a2=2, then a must be sqrt(2). So the ratio between the individual decay a1=a2 and the collective decay is sqrt(2). For our stack decay under alpha = 2, we would have for a1=a2=2, a=1/2, so the ratio between individual decay and collective decay is 4.

It’s actually quite interesting to look at these relations a bit deeper, and see how the “Pythagorean” (geometric) relationship evolves as we change alpha from something like alpha<=1/2 to alpha>=2.

If we take alpha going to 2 and above, we have the effect of much slower collective decay than 4x compared to the individual decay. Physically this corresponds to the situation when the delay of an inverter in the ring becomes strongly inversely proportional to voltage. Geometrically, this is like contracting the height of the triangle in which sides go further apart than 90 degrees – say the triangle is isosceles for simplicity, and say its angle is say 100 degrees.

The case of alpha = 1/2 corresponds to the case where delay is proportional to the square root of Voltage, and here the stack makes the decay rate to follow the inverse Pythagorean! So this is the case of a triangle with sides being at 90 degrees.

But if alpha goes below 1/2, we have the  effect of the collective decay being closer to individual decays, and geometrically the height of the triangle where sides close up to less than 90 degrees!

Incidentally, Andrey Mokhov suggested we may consider a different physical interpretation for inverse Pythagorean. Instead of looking at lengths a, b and h, one can consider volumes Va, Vb and Vh of 4-D cubes with such side lengths. Then these volumes would relate exactly as in our case of alpha=2, i.e. 1/sqrt (Vh)=1/sqrt(Va)+1/sqrt(Vb).

Cool!


Charge decay in a stack of two digital circuits follows inverse Pythagorean Law!

Posted on by
Reply

My last blog about my talk at HDT 2019 on Stacking Asynchronous Circuits contained a link to my slides. I recommend you having a particular look at slide #21. It talks about an interesting fact that a series (stack) discharge rate follows the law of the inverse Pythagorean!

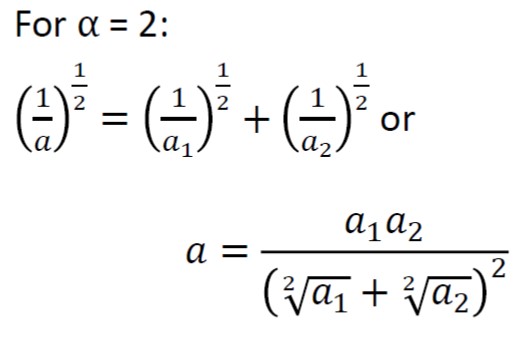
It looks like mother nature caters for a geometric law of the most economic common between two individual sides.

My Talk on Stacked Asynchronous Circuits at HDT 2019

Posted on by
Reply

I just attended a Second Workshop on Hardware Design Theory, held in Budapest, collocated with 33rd International Symposium on Distributed Computing http://www.disc-conference.org/wp/disc2019/

The HDT’19 workshop was organised by Moti Medina and Andrey Mokhov. It had a number of invited talks, and here is the programme: https://sites.google.com/view/motimedina/hdt-2019

I gave a talk on Stacked Asynchronous circuits.

Here is the abstract: In this talk we will look at digital circuits from the viewpoint of electrical circuit theory, i.e. as loads to power sources. Such circuits, especially when they are asynchronous can be seen as voltage controlled oscillators. Their switching behaviour, including their operating frequency is modulated by the supply voltage. Interestingly, in the reverse direction if they are driven by external event sources, their switching frequency determines their inherent impedance which itself makes them ideal potentiometers or voltage dividers. Such circuits can be stacked like non-linear resistors in series and parallel, and lend themselves to interesting theoretical and practical results, such as RC circuits with hyperbolic capacitor discharges and designs of dynamic frequency mirrors.

Here is the PDF of my slides: https://www.staff.ncl.ac.uk/alex.yakovlev/home.formal/stacked-async-budapest-2019.171019.pdf

Towards computing on energy current

Posted on by
Reply

My further discourse with Ed and Ivor last night has resulted in the following message from Ed.

Ed:

Alex,

your yesterday message to Ivor makes me consider once again the mathematical equations Ivor introduces in his paper “The Heaviside Signal”. I concentrate on the equation c(dE/dx) = dE/dt in Appendix 1 (ignoring the ” – ” on the right side). This formula is constructed by interpreting the propagation of a voltage step in space (first diagram) and in time (second diagram) as a velocity v of motion in the direction of time, v = dx/dt, that is, a vector quantity. In the diagrams, this velocity v is symbolized by the letter c. With dx/dt = v the equation c(dE/dx) = dE/dt results in c = dx/dt = v. This asserted equality of c and v then insinuates that the voltage step would really “travel” in space and time with a vector velocity v = c in the direction of time. As I see things, the equation v = c is mistaken, since v is a vector quantity, which c is not. c is a scalar, as is proven by the Poynting vector E when put over p, resulting in c: E/p = c. Vector E over vector p = mv; v is a vector, c is a scalar quantity. Q.e.d. So c does not symbolize some velocity of some motion in the direction of time. What else does this factor mean, as it is  undoubtedly a quotient of a quantity of space, L, over a quantity of time, T, c [L/T] ? If you draw a diagram of Cartesian coordinates, space L in the vertical axis, time T in the horizontal, and you put the elements of space, L, over the elements of time, T, you get the constant quotient [L/T] to characterize the diagram as its parameter, or “grating constant”. Evidently this constant is not a vector, but a scalar. This shows that not every quotient dx/dt [L/T] represents a velocity of propagation in time, as the vector v does it. Rather it may be the case that such a quotient, the more if it is a constant (!), just represents the parameter of the space-time frame of reference wherein an observed phenomenon like the above-mentioned voltage step takes place. And this takes us into the middle of our finding that Poynting’s energy vector E = pxc differs from the classical scalar energy E = mv^2/2. This difference, as we can see now, is a consequence of not distinguishing between velocity v (vector, and variale), and the scalar constant c. Do you agree?

Ed.   

To which I have replied the following:

Ed,

I am afraid I disagree with your conclusion that c coming out of the analysis of c(dE/dx) = dE/dt in Appendix 1  is a vector!

You raise a metaphysical story around it I am afraid.

This c is a constant coefficient. c is not a vector – its scalar.We have vectors around it dE/dt and dE/dx. These are vectors – one is force (or power in modern terms) and the other is momentum (as we agreed with you before). 

Full stop here!

Then, we should acknowledge the fact that there is a physical element behind this c – and this is energy current, which emanates in the universe from its Big Bang!

This is the carrier of interactions in Nature. This wasn’t known to Artistotle, Galileo, Newton, Maxwell … Ivor was and is the first to give this carrier the appropriate place.

If you had known a bit of the physics of communication (I recommend you to read Hans Schantz papers and book for that) you’d realise that its completely natural for communication (or interaction for that matter) to have a carrier – and this carrier for ExH does not need massed matter – it can perfectly well live in vaccuum.

That’s my take on this. You played an important role in this discourse. We have identified what momentum is in Catt’s theory and Heaviside Signal. Eureka!

What I have also discovered thanks to Ivor is the potential way for future computing – which is based NOT on envelope characteristics – such as exponentials and sines, but on discretised steps – this can potentially give way to improving the speed of computations by 2-3 orders of magnitude – we just need appropriate devices to support this speed and react to changes transmitted in energy current. I am already working on this!!!

Alex