Over the last couple of week I have been witnessing an interesting email discussion about Maxwell’s equations between 2-3 people trying to come to terms with the difficulty of accommodating the notion of displacement current in free space and ‘sorting out’ the Ampere’s law. The latter combines, for whatever reason, both the elements of propagating field (not requiring charged particles as this field can propagate without involving massed matter) and current density (implying the existence of massed particles).
I have drawn my own conclusions out of this discussion, which ended up with conclusions that the above mentioned difficulty cannot be easily resolved with the bounds the temple of the classical electromagnetics with its holy book of Maxwell’s laws.
Here are my comments on this:
To Ivor Catt:
Following your theory where the Heaviside signal travels (and can only do so) with the speed of light in the medium, such a speed is entirely determined by epsilon and mu. Thus, where we have an interface between very low epsilon dielectric and very high epsilon metal, from the point of view of energy current, we have the effect similar to friction (against the metal surface – like a rotating wheel goes forward on the ground thanks to experiencing friction against the ground). And thanks to this “friction” it prefers to trolley along the metal wire, or between the metal plates of the capacitor.
To David Tombe:
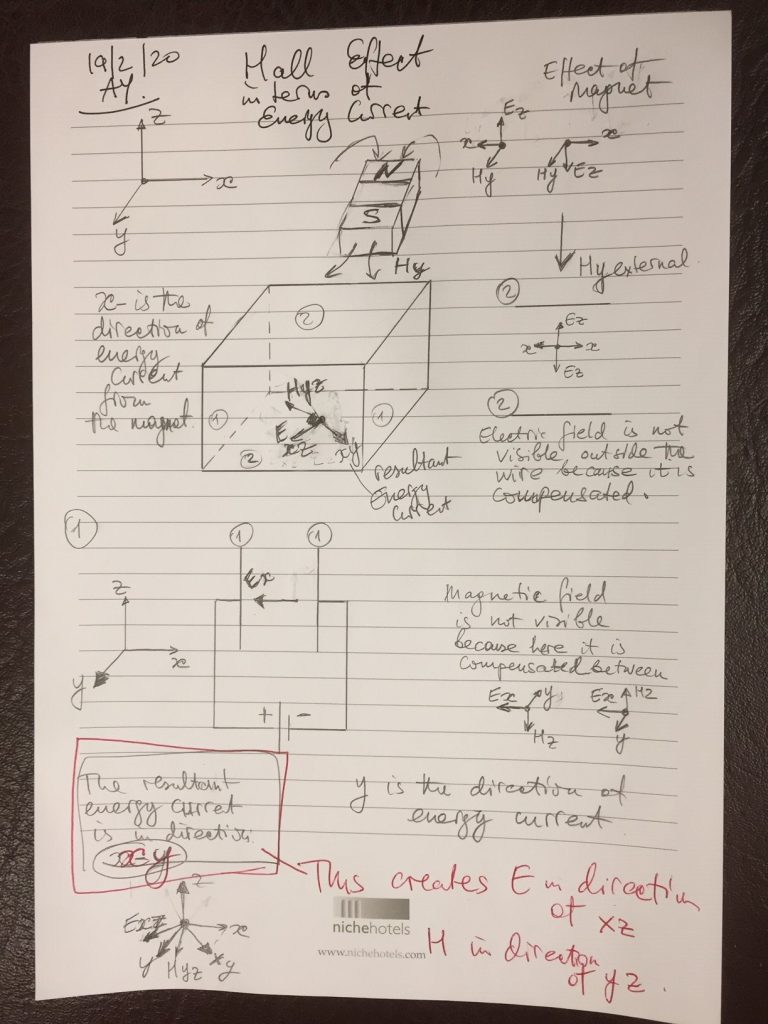
Catt’s theory works at a different level of abstraction. This is the level of fundamental energy current. This level underpins “charged particles”. The latter are the result of the ExH energy current trapped in corresponding sections of space. What’s important is that that trapped energy never stops inside those particles as it can only exist in the form of ExH slabs moving with speed of light in the epsilon-mu medium. So then, when you apply energy current travelling outside those particles, there is an interesting interaction with the energy current inside those particles.
The entire world is filled with energy current fractally sectioned into fragments determined by space sections.
All I can say is that in my opinion you misunderstand the domain of action of Catt’s theory. It does not consider static electric field. That’s it. There’s no such a thing as static EM energy. It can only move at speed c=dx/dt, in all directions.
And this energy fills up space according to its epsilon/mu properties.
There’s no need for Maxwells equations to be involved in Catt’s theory. All these equations are partial, like Greek gods.
To Ivor Catt:
I, perhaps surreptitiously, was awaiting for your email, either in public or in private.
Coincidentally, about an hour ago, I typed a message intended to be sent to the whole list from that discussion (adding Malcolm, who I think is on the same wavelength with us), saying:
“Ivor, please, say something, because these people are facing an impossible task of ‘squaring the circle’ of a set of Maxwell’s laws into something coherent – but the reason why it is impossible is that no one actually knows exactly what Maxwell meant by that list of laws dressed into fairly sophisticated mathematics. So, Ivor, the same fate may be with you, unless you say something, in some 20 years from now {well, it looks like I miscalculated by 5 years from your estimate of 2045!} no one will know exactly what Catt meant by his energy current”.
Then some invisible force pushed me to discard that email! And now, I had an evening walk to my office to freshen up my mind, and here I see your email.
Sadly, people, don’t listen and can’t liberate themselves from the heavy chains of those (partial) laws – which are like, indeed, those separate gods of Greeks or Romans being responsible for one aspect of life or another or one phenomenon in nature or another. They can’t understand that the Occam’s Razor of nature wouldn’t tolerate having so many (purportedly, fundamental) relationships, with lots of tautology in them. All those relationships, taken individually, are contrapuntal and superposing.
People can’t understand that there is no need for stationary fields, no need for separate treatment of charged particles etc. Everything comes naturally as a result of energy current trapped in sections of space, where it continues to move.
I think the next big leap where Catt’s vision will show its power will happen in high-speed computing and a massively parallel scale – truly high-speed! Until then we will probably fight against the Windmills of stale minds and deaf ears …
This confused discussion between David Tombe and Akinbo (not sure if Malcolm has seen that) is an illustration of the fact that behind the mathematically elegant façade of Maxwell’s laws there is a massive mess of physical concepts, a cacophony of man-made and contrived ‘pagan-like’ beliefs and disbeliefs (e.g., did Maxwell mean that or not?), which may work in special cases. The fact that these beliefs can work in special cases of success in growing crops or hunting/herding animals in some regions of the world, or in a more modern terms, wiring up a Victorian mansion and sending data to Mars rovers. But how they are going to succeed in the future when needs Terabit/s data rates or picosecond latency in accessing storage, nobody knows. I am less inclined in dividing people into true scientists, careerists or other categories. Historical materialism (which we had to study back in the USSR) gave pretty good explanation of all kinds of folk under the sun. Nobody is saint here. It’s just a personal comfort matter …
To Akinbo Ojo (in reply to his email attached below):
Just combine ∇2E = µε(∂2E/∂t2)
or ∇2H = µε(∂2H/∂t2)
into one eqn, replacing E and H
with ExH, and you’ll have the Heaviside signal (aka energy current) propagating
in space with speed of light in the epsilon/mu medium, and that’s all what is
needed by Catt’s theory, and that what fills up fragments of space, in order to
form transmission lines of particular Z0, capacitors, inductors, elementary
particles, etc.
Everything in the world is filled up with this energy current, and any such an entrapment of energy current turns sections of space into elements of matter (or mass)!
From: Akinbo Ojo <taojo@hotmail.com>
Sent: 14 January 2020 14:20
Subject: Re: Displacement Current in Deep Space for Starlight
Hi David,
I didn’t say
there was an error. I said given the Ampere and Faraday equations when you
follow the curls and substitutions you will confront something that would be
unpalatable to you and which you must swallow before you can get ∇2E = µε(∂2E/∂t2)
or ∇2H = µε(∂2H/∂t2).
Regards,
Akinbo